题目内容
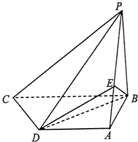 如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD.底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB.点E在棱PA上,.
如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD.底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB.点E在棱PA上,.(1)求异面直线PA与CD所成的角;
(2)点E在棱PA上,且
| PE |
| EA |
(3)在(2)的条件下求二面角A-BE-D的平面角的余弦值.
分析:(1)以点B为坐标原点,以BA为x轴,以BC为y轴,以BP为z轴,建立空间直角坐标至B-xyz,根据条件求出
和
,然后求出这两个向量的所成角即为异面直线CD与PA所成的角;
(2)要使PC∥平面EBD,只需
垂直于面BDE的一个法向量,利用向量法可求;
(3)先求平面EBD的法向量与平面ABE的法向量,然后利用向量的夹角公式求出此角的余弦值即二面角A-BE-D的大小的余弦值.
| CD |
| PD |
(2)要使PC∥平面EBD,只需
| PC |
(3)先求平面EBD的法向量与平面ABE的法向量,然后利用向量的夹角公式求出此角的余弦值即二面角A-BE-D的大小的余弦值.
解答:解析:由PB⊥底面ABCD得PB⊥AB,PB⊥BC,以
,
,
分别为x,y,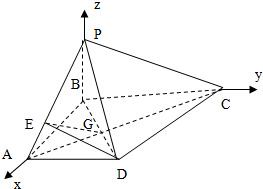
z轴的正方向建立如图所示的空间直角坐标系,不妨设AB=2,则B(0,0,0),A(2,0,0),D(2,2,0),
由PB⊥底面ABCD,PB⊥CD,CD⊥PD,PD∩PB=P,CD⊥面PBD,CD⊥BD,所以△CDB为等腰直角三角形,故DB=2
,CB=
BD=4,
∴C(0,4,0),P(0,0,2),(3分)
(1),
=(2,0,-2),
=(-2,2,0),
∴cos<
,
>=
,故异面直线PA与CD所成的角为60°; (7分)
(2)
=λ
,∴
-
=λ(
-
),∴
=
+
,
=(0,2,0),
=(0,0,2),
=(0,
,
),
=(4,0,-2),
设面BDE的一个法向量为
=(x,y,z),
∴
∴
,
令y=1,
=(-1,1,-λ),
要使PC∥平面EBD,则必须有
⊥
,∴-4+2λ=0,λ=2,所以当λ=2时PC∥平面EBD. (11分)
(3)
⊥面ABE,
=(-1,1,-2),
=(4,0,0),cos<
,
>=-
,
∴二面角A-BE-D的平面角的余弦值为
. (15分)
| BC |
| BA |
| BP |

z轴的正方向建立如图所示的空间直角坐标系,不妨设AB=2,则B(0,0,0),A(2,0,0),D(2,2,0),
由PB⊥底面ABCD,PB⊥CD,CD⊥PD,PD∩PB=P,CD⊥面PBD,CD⊥BD,所以△CDB为等腰直角三角形,故DB=2
| 2 |
| 2 |
∴C(0,4,0),P(0,0,2),(3分)
(1),
| PA |
| CD |
∴cos<
| PA |
| CD |
| 1 |
| 2 |
(2)
| PE |
| EA |
| BE |
| BP |
| BA |
| BE |
| BE |
| λ |
| 1+λ |
| BA |
| 1 |
| 1+λ |
| BP |
| BA |
| BP |
| BE |
| 2λ |
| 1+λ |
| 2 |
| 1+λ |
| PC |
设面BDE的一个法向量为
| n |
|
|
|
令y=1,
| n |
要使PC∥平面EBD,则必须有
| PC |
| n |
(3)
| BC |
| n |
| BC |
| BC |
| n |
| ||
| 6 |
∴二面角A-BE-D的平面角的余弦值为
| ||
| 6 |
点评:本题以四棱锥为载体,主要考查直线与平面的位置关系、两异面直线所成角、二面角及其平面角等有关知识,考查空间想象能力和思维能力,应用向量知识解决立体几何问题的能力.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=