题目内容
（理科）已知x＜1，则函数f(x)=x+
的最大值为（ ）
| 1 |
| x-1 |
| A、1 | B、2 | C、-1 | D、3 |
分析：先将原函数式化成：f(x)=x-1+
+1，利用基本不等式，结合端点的函数值即可求解．
| 1 |
| x-1 |
解答：解：函数ff(x)=x+
∴f(x)=x-1+
+1
已知x＜1，
∴f(x)=x-1+
+1≤-2+1=-1
∴函数f（x）最大值在x=0时取得
∴函数f(x)=x+
的最大值为-1．
故选C．
| 1 |
| x-1 |
∴f(x)=x-1+
| 1 |
| x-1 |
已知x＜1，
∴f(x)=x-1+
| 1 |
| x-1 |
∴函数f（x）最大值在x=0时取得
∴函数f(x)=x+
| 1 |
| x-1 |
故选C．
点评：本题考查基本不等式在求最值中的应用，解答的关键是对于原函数式适当配凑，属于基础题．
练习册系列答案
相关题目
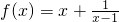的最大值为
的最大值为（ ）