题目内容
(2012•虹口区二模)已知:曲线C上任意一点到点F
的距离与到直线x=-1的距离相等.
(1)求曲线C的方程;
(2)过点F
作直线交曲线C于M,N两点,若|MN|长为
,求直线MN的方程;
(3)设O为坐标原点,如果直线y=k(x-1)交曲线C于A、B两点,是否存在实数k,使得
•
=0?若存在,求出k的值;若不存在,说明理由.
|
(1)求曲线C的方程;
(2)过点F
|
| 16 |
| 3 |
(3)设O为坐标原点,如果直线y=k(x-1)交曲线C于A、B两点,是否存在实数k,使得
| OA |
| OB |
分析:(1)根据曲线C上任意一点到点F
的距离与到直线x=-1的距离相等,可知曲线为抛物线,焦点在x轴上,且p=2,从而可得曲线C的方程;
(2)当直线MN的斜率不存在时,不合题意;当直线MN的斜率存在时,设MN:y=k(x-1),代入y2=4x,利用|MN|长为
,建立方程,即可求得直线MN的方程;
(3)将y=k(x-1),代入y2=4x,得k2x2-2(k2+2)x+k2=0,验证x1x2+y1y2=-3≠0,故不存在满足条件的k.
|
(2)当直线MN的斜率不存在时,不合题意;当直线MN的斜率存在时,设MN:y=k(x-1),代入y2=4x,利用|MN|长为
| 16 |
| 3 |
(3)将y=k(x-1),代入y2=4x,得k2x2-2(k2+2)x+k2=0,验证x1x2+y1y2=-3≠0,故不存在满足条件的k.
解答:解:(1)∵曲线C上任意一点到点F
的距离与到直线x=-1的距离相等
∴曲线为抛物线,焦点在x轴上,且p=2
∴曲线C的方程为y2=4x…(4分)
(2)当直线MN的斜率不存在时,不合题意.…(5分)
当直线MN的斜率存在时,设MN:y=k(x-1),代入y2=4x,得k2x2-2(k2+2)x+k2=0…(7分)
记M(x1,y1),N(x2,y2),∴x1x2=1,x1+x2=
,
∵|MN|长为
,
∴
=
•
,
解得k=±
…(10分)
∴直线MN:y=±
(x-1)…(11分)
(3)将y=k(x-1),代入y2=4x,得k2x2-2(k2+2)x+k2=0
记A(x1,y1),B(x2,y2),∴x1x2=1,x1+x2=
,…(13分)∴y1y2=k2(x1-1)(x2-1)=k2[x1x2-(x1+x2)+1]=-4…(15分)
∴x1x2+y1y2=-3≠0,
∴
•
≠0,∴不存在满足条件的k.…(18分)
|
∴曲线为抛物线,焦点在x轴上,且p=2
∴曲线C的方程为y2=4x…(4分)
(2)当直线MN的斜率不存在时,不合题意.…(5分)
当直线MN的斜率存在时,设MN:y=k(x-1),代入y2=4x,得k2x2-2(k2+2)x+k2=0…(7分)
记M(x1,y1),N(x2,y2),∴x1x2=1,x1+x2=
| 2(k2+2) |
| k2 |
∵|MN|长为
| 16 |
| 3 |
∴
| 16 |
| 3 |
| 1+k2 |
[
|
解得k=±
| 3 |
∴直线MN:y=±
| 3 |
(3)将y=k(x-1),代入y2=4x,得k2x2-2(k2+2)x+k2=0
记A(x1,y1),B(x2,y2),∴x1x2=1,x1+x2=
| 2(k2+2) |
| k2 |
∴x1x2+y1y2=-3≠0,
∴
| OA |
| OB |
点评:本题考查抛物线的定义,考查曲线的方程,考查直线与抛物线的位置关系,解题的关键是直线与抛物线联立,利用韦达定理进行解题.

练习册系列答案
相关题目
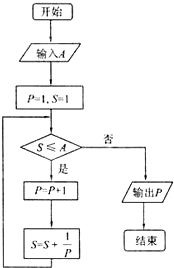 (2012•虹口区二模)执行如图所示的程序框图,若输入A的值为2,则输出P的值为
(2012•虹口区二模)执行如图所示的程序框图,若输入A的值为2,则输出P的值为