题目内容
(2012•虹口区二模)函数f(x)=
,则不等式f(2-x2)>f(x)的解集是
|
(-2,1)
(-2,1)
.分析:由y1=x2+4x在[0,+∞)上单调递增,y2=4x-x2在(-∞,0)上单调递增,且y1最小值=0≥y2最大值=0,则函数f(x)在R上单调递增,可得2-x2>x,解不等式可求
解答:解:由y1=x2+4x在[0,+∞)上单调递增,y2=4x-x2在(-∞,0)上单调递增,
且y1最小值=0≥y2最大值=0
由分段函数的性质可知,函数f(x)在R上单调递增
∵f(2-x2)>f(x)
∴2-x2>x整理可得,x2+x-2<0
解可得,-2<x<1
故答案为(-2,1)
且y1最小值=0≥y2最大值=0
由分段函数的性质可知,函数f(x)在R上单调递增
∵f(2-x2)>f(x)
∴2-x2>x整理可得,x2+x-2<0
解可得,-2<x<1
故答案为(-2,1)
点评:本题主要考查了利用分段函数的单调性求解不等式,解题的关键是灵活利用二次函数的性质确定函数的单调性

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
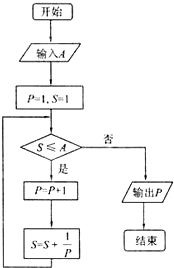 (2012•虹口区二模)执行如图所示的程序框图,若输入A的值为2,则输出P的值为
(2012•虹口区二模)执行如图所示的程序框图,若输入A的值为2,则输出P的值为