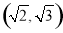题目内容
设双曲线 的右焦点为
的右焦点为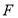 ,右顶点为
,右顶点为 ,过
,过 作
作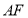 的垂线与双曲线的两条渐近线交于
的垂线与双曲线的两条渐近线交于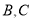 两点,过
两点,过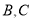 分别作
分别作 的垂线,两垂线交于点
的垂线,两垂线交于点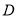 .若
.若 到直线
到直线 的距离小于
的距离小于 ,则该双曲线的离心率的取值范围是( )
,则该双曲线的离心率的取值范围是( )
A. B.
B.
C.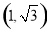 D.
D.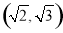
练习册系列答案
相关题目
题目内容
设双曲线 的右焦点为
的右焦点为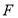 ,右顶点为
,右顶点为 ,过
,过 作
作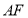 的垂线与双曲线的两条渐近线交于
的垂线与双曲线的两条渐近线交于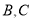 两点,过
两点,过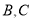 分别作
分别作 的垂线,两垂线交于点
的垂线,两垂线交于点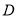 .若
.若 到直线
到直线 的距离小于
的距离小于 ,则该双曲线的离心率的取值范围是( )
,则该双曲线的离心率的取值范围是( )
A. B.
B.
C.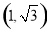 D.
D.