题目内容
【题目】已知椭圆的方程为![]() ,其离心率
,其离心率![]() ,且短轴的个端点与两焦点组成的三角形面积为
,且短轴的个端点与两焦点组成的三角形面积为![]() ,过椭圆上的点
,过椭圆上的点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 满足
满足![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() 相切,且交椭圆于
相切,且交椭圆于![]() 两点,
两点, ![]() ,记
,记![]() 的面积为
的面积为![]() ,
, ![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值 .
的最大值 .
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)根据题意可得椭圆的方程为![]() ,设
,设![]() ,
,
由![]() ,得
,得![]() ,根据代入法可得曲线
,根据代入法可得曲线![]() 的方程为
的方程为![]() .(2)由题知直线
.(2)由题知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,由
,由![]() 与圆相切可得
与圆相切可得![]() .将
.将![]() 与
与![]() 联立可得二次方程,然后由根与系数的关系及弦长公式可得
联立可得二次方程,然后由根与系数的关系及弦长公式可得![]() ,从而得到
,从而得到![]() ,
,![]() ,求得
,求得![]() 后再根据基本不等式求解即可得到所求.
后再根据基本不等式求解即可得到所求.
(1)依题意可得![]()
![]() ,
,
由![]() ,
,
解得![]() ,椭圆方程为
,椭圆方程为![]() .
.
设![]() ,
,
由![]() ,得
,得![]() ,
,
代人椭圆方程得曲线![]() 的方程为
的方程为![]() .
.
(2)由题知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,
,
由![]() 与圆相切可得
与圆相切可得![]() ,即
,即![]() .
.
由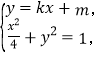 消
消![]() 整理得
整理得![]()
![]()
又直线![]() 与椭圆交于
与椭圆交于![]() 两点,
两点,
所以![]() ,故得
,故得![]() .
.
设![]() ,
,
则![]() ,
,![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
则![]() ,
,![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
当且仅当![]() ,即
,即![]() 时,等号成立.
时,等号成立.
所以![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
相关题目
【题目】为考察某种药物预防疾病的效果,进行动物试验,得到如下药物效果与动物试验列联表:
患病 | 未患病 | 总计 | |
服用药 | 10 | 45 | 55 |
没服用药 | 20 | 30 | 50 |
总计 | 30 | 75 | 105 |
经过计算,![]() ,根据这一数据分析,下列说法正确的是
,根据这一数据分析,下列说法正确的是
临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A. 有97.5%的把握认为服药情况与是否患病之间有关系
B. 有99%的把握认为服药情况与是否患病之间有关系
C. 有99.5%的把握认为服药情况与是否患病之间有关系
D. 没有理由认为服药情况与是否患病之间有关系

