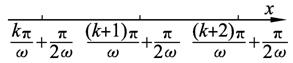题目内容
ω是正实数,设Sω={θ|f(x)=sin[ω(x+θ)]是偶函数},若对每个实数a,Sω∩(a,a+1)的元素不超过2个,且有a使Sω∩(a,a+1)含2个元素,则ω的取值范围是
(π,2π]
(π,2π]
.分析:依题意,ωθ=kπ+
(k∈Z)?θ=
+
(k∈Z),于是相邻两θ的距离为
,依题意
≤
<1,从而可得ω的取值范围.
| π |
| 2 |
| kπ |
| ω |
| π |
| 2ω |
| π |
| ω |
| 1 |
| 2 |
| π |
| ω |
解答:解:要使f(x)=sin[ω(x+θ)]是偶函数,则ωθ=
+kπ,k∈Z,∴θ=
+
(k∈Z),
∴相邻两θ的距离为
.
∵Sω∩(a,a+1)的元素不超过2个,且有a使Sω∩(a,a+1)含2个元素,
∴
≤
<1.
∴1<
≤2.
∴π<ω≤2π.
∴ω的取值范围是(π,2π].
故答案为:(π,2π].
| π |
| 2 |
| π |
| 2ω |
| kπ |
| ω |
∴相邻两θ的距离为
| π |
| ω |
∵Sω∩(a,a+1)的元素不超过2个,且有a使Sω∩(a,a+1)含2个元素,
∴
| 1 |
| 2 |
| π |
| ω |
∴1<
| ω |
| π |
∴π<ω≤2π.
∴ω的取值范围是(π,2π].
故答案为:(π,2π].
点评:本题考查正弦函数的奇偶性,考查交集及其运算,得到
≤
<1是关键,突出考查抽象思维与逻辑思维,属于难题.
| 1 |
| 2 |
| π |
| ω |

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目