题目内容
已知向量m=(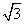 sin2x-1,cosx),n=(
sin2x-1,cosx),n=(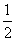 ,cosx),设函数f(x)=m·n,
,cosx),设函数f(x)=m·n,
(1)求函数f(x)的最小正周期及在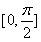 上的最大值;
上的最大值;
(2)已知△ABC的角A、B、C所对的边分别为a、b、c,A、B为锐角,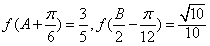 ,又a+b=
,又a+b=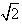 +1,求a、b、c的值.
+1,求a、b、c的值.
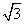 sin2x-1,cosx),n=(
sin2x-1,cosx),n=(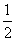 ,cosx),设函数f(x)=m·n,
,cosx),设函数f(x)=m·n,(1)求函数f(x)的最小正周期及在
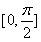 上的最大值;
上的最大值;(2)已知△ABC的角A、B、C所对的边分别为a、b、c,A、B为锐角,
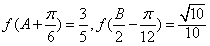 ,又a+b=
,又a+b=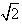 +1,求a、b、c的值.
+1,求a、b、c的值.解:(1) ,
,
∴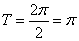 ,
,
由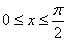 得
得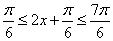 ,
,
∴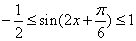 ,
,
∴ 。
。
(2)∵ ,
,
∴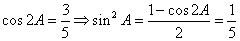 ,
,
∵A为锐角,
∴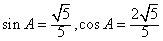 ,
,
又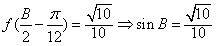 ,
,
∵B为锐角,
∴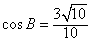 ,
,
由正弦定理知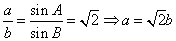 ,
,
又a+b=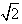 +1
+1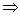
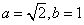 ,
,
又∵sinC=sin(A+B)=sinA·cosB+cosA·sinB=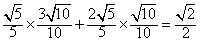 ,
,
由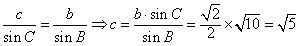 。
。
 ,
,∴
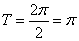 ,
,由
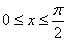 得
得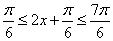 ,
,∴
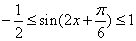 ,
,∴
 。
。(2)∵
 ,
,∴
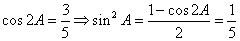 ,
,∵A为锐角,
∴
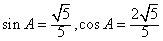 ,
,又
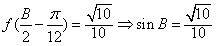 ,
,∵B为锐角,
∴
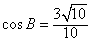 ,
,由正弦定理知
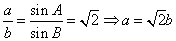 ,
,又a+b=
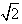 +1
+1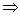
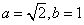 ,
,又∵sinC=sin(A+B)=sinA·cosB+cosA·sinB=
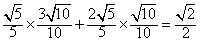 ,
,由
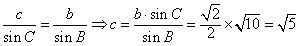 。
。 
练习册系列答案
相关题目