题目内容
设函数f(x)=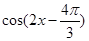 +2cos2x.
+2cos2x.
(1)求f(x)的最大值,并写出使f(x)取最大值时x的集合;
(2)已知△ABC中,角A,B,C的对边分别为a,b,c,若f(B+C)=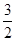 ,b+c=2,求a的最小值.
,b+c=2,求a的最小值.
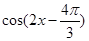 +2cos2x.
+2cos2x.(1)求f(x)的最大值,并写出使f(x)取最大值时x的集合;
(2)已知△ABC中,角A,B,C的对边分别为a,b,c,若f(B+C)=
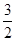 ,b+c=2,求a的最小值.
,b+c=2,求a的最小值.(1){x|x=kπ-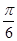 ,k∈Z}.(2)1
,k∈Z}.(2)1
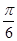 ,k∈Z}.(2)1
,k∈Z}.(2)1(1)∵f(x)=cos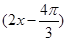 +2cos2x=cos
+2cos2x=cos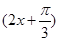 +1,
+1,
∴f(x)的最大值为2.
f(x)取最大值时,cos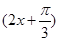 =1,2x+
=1,2x+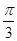 =2kπ(k∈Z),
=2kπ(k∈Z),
故x的集合为{x|x=kπ-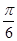 ,k∈Z}.
,k∈Z}.
(2)由f(B+C)=cos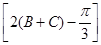 +1=
+1=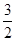 ,可得cos
,可得cos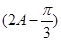 =
=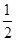 ,
,
由A∈(0,π),可得A=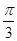 .在△ABC中,由余弦定理,
.在△ABC中,由余弦定理,
得a2=b2+c2-2bccos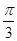 =(b+c)2-3bc,
=(b+c)2-3bc,
由b+c=2知bc≤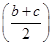 2=1,当b=c=1时bc取最大值,此时a取最小值1.
2=1,当b=c=1时bc取最大值,此时a取最小值1.
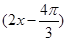 +2cos2x=cos
+2cos2x=cos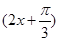 +1,
+1,∴f(x)的最大值为2.
f(x)取最大值时,cos
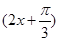 =1,2x+
=1,2x+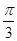 =2kπ(k∈Z),
=2kπ(k∈Z),故x的集合为{x|x=kπ-
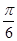 ,k∈Z}.
,k∈Z}.(2)由f(B+C)=cos
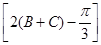 +1=
+1=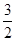 ,可得cos
,可得cos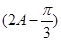 =
=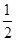 ,
,由A∈(0,π),可得A=
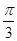 .在△ABC中,由余弦定理,
.在△ABC中,由余弦定理,得a2=b2+c2-2bccos
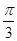 =(b+c)2-3bc,
=(b+c)2-3bc,由b+c=2知bc≤
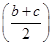 2=1,当b=c=1时bc取最大值,此时a取最小值1.
2=1,当b=c=1时bc取最大值,此时a取最小值1.
练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
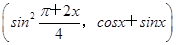 ,b=(4sinx,cosx-sinx),f(x)=a·b.
,b=(4sinx,cosx-sinx),f(x)=a·b.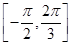 上是增函数,求ω的取值范围;
上是增函数,求ω的取值范围;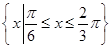 ,B={x||f(x)-m|<2},若A
,B={x||f(x)-m|<2},若A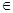 B,求实数m的取值范围.
B,求实数m的取值范围.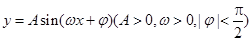 的最小值为
的最小值为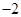 ,其图像相邻最高点与最低点横坐标之差为
,其图像相邻最高点与最低点横坐标之差为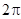 ,且图像过点(0,1),则其解析式是( )
,且图像过点(0,1),则其解析式是( )



 π
π π
π 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是____________________.
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是____________________.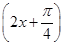 和函数y=cos
和函数y=cos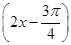 的图象关于原点对称;命题q:当x=kπ+
的图象关于原点对称;命题q:当x=kπ+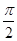 (k∈Z)时,函数y=
(k∈Z)时,函数y=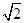 (sin 2x+cos 2x)取得极小值.下列说法正确的是( )
(sin 2x+cos 2x)取得极小值.下列说法正确的是( )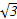 sinxcosx-1(x∈R).
sinxcosx-1(x∈R).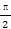 ],求函数f(x)的最大值与最小值.
],求函数f(x)的最大值与最小值. 与函数g(x)=cos
与函数g(x)=cos ,下列说法正确的是( )
,下列说法正确的是( ) 对称
对称 x3+
x3+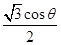 x2,其中θ∈
x2,其中θ∈ ,则导数f ′(1)的取值范围是_______.
,则导数f ′(1)的取值范围是_______.