题目内容
已知函数 ,
,(1)求f(x)的定义域和值域;
(2)讨论f(x)的奇偶性;
(3)讨论f(x)的单调性.
【答案】分析:(1)求f(x)的定义域可令分母2x+1≠0求解,对函数的解析式进行变化,判断出值域即可值域;
(2)讨论f(x)的奇偶性并证明,本函数是一个奇函数,由定义法证明即可;
(3)判断f(x)在(0,+∞)的单调性并证明,由解析式可以看出本函数在(0,+∞)是一个减函数,可由复合函数的单调性的判断方法判断证明即可.
解答:解:(1)令分母2x+1≠0解得x≠0,故定义域为R
函数的解析式可以变为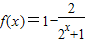 ,由于2x+1>1,故 1>
,由于2x+1>1,故 1>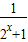 >0
>0
故2>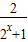 >0
>0
∴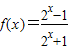 的取值范围是(-1,1)
的取值范围是(-1,1)
(2)函数是一个奇函数,证明如下
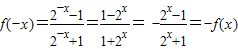 ,故是一个奇函数.
,故是一个奇函数.
(3)先证f(x)在(0,+∞)是一个减函数,证明如下
由于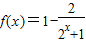 ,在(0,+∞)上,2x+1递增且函数值大于0,
,在(0,+∞)上,2x+1递增且函数值大于0,
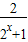 在(0,+∞)上是减函数,故
在(0,+∞)上是减函数,故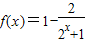 ,在(0,+∞)上是增函数,
,在(0,+∞)上是增函数,
又因为f(x)是奇函数,且f(0)=0,所以f(x)在(-∞,+∞)是一个增函数.
点评:本题考查函数单调性的、奇偶性的判断与证明以及函数的定义域与值域的求法,求解此类题的关键是对函数性质的证明方法了然于胸,熟知其各种判断证明方法.
(2)讨论f(x)的奇偶性并证明,本函数是一个奇函数,由定义法证明即可;
(3)判断f(x)在(0,+∞)的单调性并证明,由解析式可以看出本函数在(0,+∞)是一个减函数,可由复合函数的单调性的判断方法判断证明即可.
解答:解:(1)令分母2x+1≠0解得x≠0,故定义域为R
函数的解析式可以变为
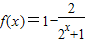 ,由于2x+1>1,故 1>
,由于2x+1>1,故 1>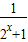 >0
>0故2>
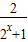 >0
>0∴
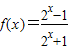 的取值范围是(-1,1)
的取值范围是(-1,1)(2)函数是一个奇函数,证明如下
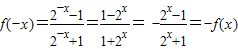 ,故是一个奇函数.
,故是一个奇函数.(3)先证f(x)在(0,+∞)是一个减函数,证明如下
由于
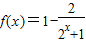 ,在(0,+∞)上,2x+1递增且函数值大于0,
,在(0,+∞)上,2x+1递增且函数值大于0,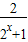 在(0,+∞)上是减函数,故
在(0,+∞)上是减函数,故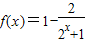 ,在(0,+∞)上是增函数,
,在(0,+∞)上是增函数,又因为f(x)是奇函数,且f(0)=0,所以f(x)在(-∞,+∞)是一个增函数.
点评:本题考查函数单调性的、奇偶性的判断与证明以及函数的定义域与值域的求法,求解此类题的关键是对函数性质的证明方法了然于胸,熟知其各种判断证明方法.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
 .
. .
. 的图象在x轴上方?
的图象在x轴上方? .
. 为f(x)的一个零点,求sin2x的值.
为f(x)的一个零点,求sin2x的值.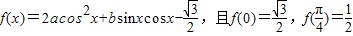 .
. .
. ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.