题目内容
已知函数 .
.(1)求f(f(3))的值;
(2)判断函数在(1,+∞)上单调性,并用定义加以证明.
(3)当x取什么值时,
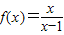 的图象在x轴上方?
的图象在x轴上方?
【答案】分析:(1)运用函数解析式,代入计算,即可求得结论;
(2)函数在(1,+∞)上单调递减,再运用定义法进行证明;
(3)转化为具体不等式,即可求得结论.
解答:解:(1)由题意,f(3)= ,∴
,∴ …(2分)
…(2分)
(2)函数在(1,+∞)上单调递减…(3分)
证明:设x1,x2是(1,+∞)上的任意两个实数,且x1<x2,则△x=x1-x2<0 …(6分)
…(6分)
由x1,x2∈(1,+∞),得(x1-1)(x2-1)>0,且x2-x1=△x>0
于是△y>0
所以, 在(1,+∞)上是减函数…(8分)
在(1,+∞)上是减函数…(8分)
(3) 得x>1或x<0…(10分)
得x>1或x<0…(10分)
点评:本题考查函数的单调性,考查解不等式,考查学生的计算能力,属于中档题.
(2)函数在(1,+∞)上单调递减,再运用定义法进行证明;
(3)转化为具体不等式,即可求得结论.
解答:解:(1)由题意,f(3)=
 ,∴
,∴ …(2分)
…(2分)(2)函数在(1,+∞)上单调递减…(3分)
证明:设x1,x2是(1,+∞)上的任意两个实数,且x1<x2,则△x=x1-x2<0
 …(6分)
…(6分)由x1,x2∈(1,+∞),得(x1-1)(x2-1)>0,且x2-x1=△x>0
于是△y>0
所以,
 在(1,+∞)上是减函数…(8分)
在(1,+∞)上是减函数…(8分)(3)
 得x>1或x<0…(10分)
得x>1或x<0…(10分)点评:本题考查函数的单调性,考查解不等式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
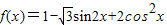 .
. .
.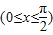 为f(x)的一个零点,求sin2x的值.
为f(x)的一个零点,求sin2x的值.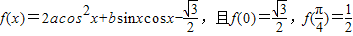 .
. .
. ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.