题目内容
已知函数 .
.(1)求f(x)的最小正周期及对称中心;
(2)若
 ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.
【答案】分析:(1)先通过两角和公式对函数解析式进行化简,得f(x)=2sin(2x+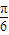 ),根据正弦函数的周期性和对称性可的f(x)的最小正周期及对称中心.
),根据正弦函数的周期性和对称性可的f(x)的最小正周期及对称中心.
(2)根据正弦函数的单调性及x的取值范围进而求得函数的最值.
解答:解:(1)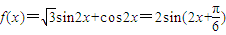
∴f(x)的最小正周期为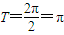 ,
,
令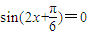 ,则
,则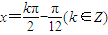 ,
,
∴f(x)的对称中心为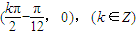 ;
;
(2)∵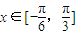 ∴
∴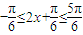
∴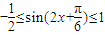
∴-1≤f(x)≤2
∴当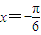 时,f(x)的最小值为-1;
时,f(x)的最小值为-1;
当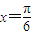 时,f(x)的最大值为2.
时,f(x)的最大值为2.
点评:本题主要考查了正弦函数的性质.三角函数的单调性、周期性、对称性等性质是近几年高考的重点,平时应加强这方面的训练.
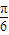 ),根据正弦函数的周期性和对称性可的f(x)的最小正周期及对称中心.
),根据正弦函数的周期性和对称性可的f(x)的最小正周期及对称中心.(2)根据正弦函数的单调性及x的取值范围进而求得函数的最值.
解答:解:(1)
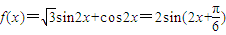
∴f(x)的最小正周期为
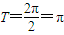 ,
,令
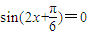 ,则
,则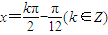 ,
,∴f(x)的对称中心为
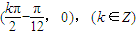 ;
;(2)∵
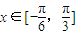 ∴
∴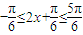
∴
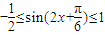
∴-1≤f(x)≤2
∴当
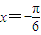 时,f(x)的最小值为-1;
时,f(x)的最小值为-1;当
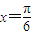 时,f(x)的最大值为2.
时,f(x)的最大值为2.点评:本题主要考查了正弦函数的性质.三角函数的单调性、周期性、对称性等性质是近几年高考的重点,平时应加强这方面的训练.

练习册系列答案
相关题目
 .
. .
. 的图象在x轴上方?
的图象在x轴上方? .
. 为f(x)的一个零点,求sin2x的值.
为f(x)的一个零点,求sin2x的值.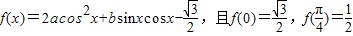 .
.