题目内容
10．已知集合A={x∈N+|$\frac{4}{x-4}$∈Z}，则集合A中元素的个数为（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
分析 将符合条件的x的值代入$\frac{4}{x-4}$计算即可．
解答 解：x=2时：$\frac{4}{2-4}$=-2，
x=3时：$\frac{4}{3-4}$=-4，
x=5时：$\frac{4}{5-4}$=4，
x=6时：$\frac{4}{6-4}$=2，
x=8时：$\frac{4}{8-4}$=1，
故选：C．
点评 本题考查了元素和集合的关系，是一道基础题．
练习册系列答案
状元及第系列答案
同步奥数系列答案
相关题目
20．（理） 曲线C：y=x3（x≥0）在点x=1处的切线为l，则由曲线C、直线l及x轴围成的封闭图形的面积是（ ）
| A． | 1 | B． | $\frac{1}{12}$ | C． | $\frac{4}{3}$ | D． | $\frac{3}{4}$ |
1．已知下列各组命题，其中p是q的充分必要条件的是（ ）
| A． | p：m≤-2或m≥6；q：y=x2+mx+m+3有两个不同的零点 | |
| B． | p：$\frac{f（-x）}{f（x）}$=1；q：y=f（x）是偶函数 | |
| C． | p：cos α=cos β；q：tan α=tan β | |
| D． | p：A∩B=A；q：A⊆U，B⊆U，∁UB⊆∁UA |
5．
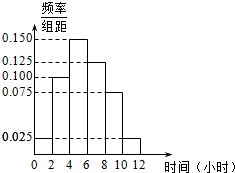某高校共有学生15 000人，其中男生10 500人，女生4500人．为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集300位学生每周平均体育运动时间的样本数据（单位：小时）．
（1）应收集多少位女生的样本数据？
（2）根据这300个样本数据，得到学生每周平均体育运动时间的频率分布直方图（如图示），在样本数据中，有60位女生的每周平均体育运动时间超过4小时，请完成每周平均体育运动时间与性别列联表，并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”．
附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．
某高校共有学生15 000人，其中男生10 500人，女生4500人．为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集300位学生每周平均体育运动时间的样本数据（单位：小时）．（1）应收集多少位女生的样本数据？
（2）根据这300个样本数据，得到学生每周平均体育运动时间的频率分布直方图（如图示），在样本数据中，有60位女生的每周平均体育运动时间超过4小时，请完成每周平均体育运动时间与性别列联表，并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”．
| P（K2≥k0） | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
2．已知-个三棱锥与一个四棱锥，它们的所有棱为1，将三棱锥与四棱锥的侧面粘在一起使之完全重合，则所得到的多面体是（ ）
| A． | 五面体 | B． | 六面体 | C． | 七面体 | D． | 八面体 |