题目内容
5. 某高校共有学生15 000人,其中男生10 500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
某高校共有学生15 000人,其中男生10 500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).(1)应收集多少位女生的样本数据?
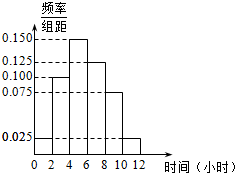
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图示),在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
分析 (1)根据15000人,其中男生10500人,女生4500人,可得应收集多少位女生的样本数据;
(2)写出2×2列联表,求出K2,与临界值比较,即可得出结论.
解答 解:(1)300×$\frac{4500}{15000}$=90,所以应收集90位女生的样本数据.------------------(4分)
(2)300位学生中有300×0.75=225(位)的每周平均体育运动时间超过4小时,75人的每周平均体育运动时间不超过4小时.又因为样本数据中有210份是关于男生的,90份是关于女生的,所以每周平均体育运动时间与性别列联表如下:
| 男生 | 女生 | 总计 | |
| 每周平均体育运动时间不超过4小时 | 45 | 30 | 75 |
| 每周平均体育运动时间超过4小时 | 165 | 60 | 225 |
| 总计 | 210 | 90 | 300 |
结合列联表可算得K2=$\frac{300×(45×60-165×30)^{2}}{210×90×75×225}$≈4.762>3.841,(10分)
所以有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.---(12分)
点评 本题主要考查独立性检验等基础知识,考查数形结合能力、运算求解能力以及应用用意识,考查必然与或然思想等,属于中档题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
15.“x>0”是“x2>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.函数f(x)=$\frac{1}{\sqrt{a{x}^{2}-4ax+3}}$的值域为(0,+∞)则a的取值范围是( )
| A. | (0,$\frac{3}{4}$) | B. | [0,$\frac{3}{4}$) | C. | [$\frac{3}{4}$,+∞) | D. | [$\frac{3}{4}$,+∞)∪(-∞,0] |
10.已知集合A={x∈N+|$\frac{4}{x-4}$∈Z},则集合A中元素的个数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
17.下面给出四个论断:①{0}是空集;②若a∈N,则-a∉N;③集合A={x∈R|x2-2x+1=0}有两个元素;④集合$B=\{x∈Q|\frac{6}{x}∈N\}$是有限集.其中正确的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
15.设函数f(x)=2x+$\frac{1}{x}$-1(x<0),则f(x)( )
| A. | 有最小值$2\sqrt{2}-1$ | B. | 有最小值$-(2\sqrt{2}+1)$ | C. | 有最大值$2\sqrt{2}-1$ | D. | 有最大值$-(2\sqrt{2}+1)$ |