题目内容
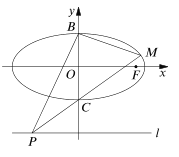
【题目】在四棱锥P﹣ABCD中，PA⊥平面ABCD，△ABC是正三角形，AC与BD的交点M恰好是AC中点，又PA=4，AB=4 
，∠CDA=120°，点N在线段PB上，且PN=2． 
（1）求证：BD⊥PC；
（2）求证：MN∥平面PDC；
（3）求二面角A﹣PC﹣B的余弦值．
【答案】
（1）证明：∵△ABC是正三角形，M是AC中点，
∴BM⊥AC，即BD⊥AC，
又∵PA⊥平面ABCD，∴PA⊥BD，
又PA∩AC=A，∴BD⊥平面PAC，
∴BD⊥PC．
（2）证明：在正△ABC中，BM=6，
在△ACD中，∵M为AC中点，DM⊥AC，∴AD=CD，
∠ADC=120°，∴DM=2，
∴ 
= 
，
在Rt△PAB中，PA=4，AB=4 
，PB=8．
∴ 
= = ，∴MN∥PD，
又MN平面PDC，PD平面平面PDC，
∴MN∥平面PDC．
（3）解：∵∠BAD=∠BAC+∠CAD=90°，
∴AB⊥AD，以A为坐标原点，分别以AB、AD、AP所在直线为x轴，y轴，z轴，建立空间直角坐标系，
∴B（4 ，0，0），C（2 ，6，0），D（0，4，0），P（0，0，4），
=（2 ，6，﹣4）， 
=（4 ，0，﹣4），
由（2）知 
=（4 ，﹣4，0）是平面PAC的法向量，
设平面PBC的一个法向量为 
=（x，y，z），
则 
，即 
，取z=3，得 =（ 
），
设二面角A﹣PC﹣B的平面角为θ，
则cosθ= 
= 
= 
，
∴二面角A﹣PC﹣B的余弦值为 ．
【解析】（1）推导出BD⊥AC，PA⊥BD，从而BD⊥平面PAC，由此能证明BD⊥PC．（2）推导出DM⊥AC，AD=CD，DM=2， = 
，从而MN∥PD，由此能证明MN∥平面PDC．（3）以A为坐标原点，分别以AB、AD、AP所在直线为x轴，y轴，z轴，建立空间直角坐标系，利用向量法能求出二面角A﹣PC﹣B的余弦值．
