题目内容

已知向量
an
=（cos2nθ，sinnθ），
bn
=（1，2sinnθ）（n∈N*），若Cn=
an
•
bn
+2n，
（1）求数列{Cn}的通项公式；
（2）求数列{Cn}的前n项和Sn．
考点：数列与三角函数的综合,平面向量数量积的运算,任意角的概念
专题：三角函数的图像与性质
分析：（1）由已知利用向量的数量积和三角函数的性质得Cn=
an
•
bn
+2n=cos2nθ+2sin2nθ+2n=2n+1，n∈N*．
（2）利用分组求和法能求出数列{Cn}的前n项和Sn．
解答： 解：（1）∵向量
an
=（cos2nθ，sinnθ），
bn
=（1，2sinnθ）（n∈N*），
∴Cn=
an
•
bn
+2n=cos2nθ+2sin2nθ+2n=2n+1，n∈N*．
（2）Sn=（2+22+23+…+2n+n
=
2(1-2n)
1-2
+n
=2n+1+n-2，n∈N*．
点评：本题考查数列的通项公式的求法，考查数列的前n项和的求法，是中档题，解题时要注意分组求和法的合理运用．
练习册系列答案
相关题目
下列各角中，为第三象限的角是（　　）
A、270°B、690°
C、-129°D、-230°
已知全集U=R，集合A={-1，2}，B={x|mx+1＞0}，若（∁UB）∩A=∅，求实数m的取值范围．
已知函数f（x）=sinx-cosx，x∈R
（1）当x∈[0，
π
2
]时，求f（x）的最大值和最小值；
（2）求f（x）的单调递减区间．
已知直线l：y=x+2，一个圆的圆心C在x轴上且该圆与y轴相切，该圆经过点A（-1，2）．则圆C的方程为
 
；直线l被圆截得的弦长等于
 
．
已知抛物线C：y2=2px（p＞0）的准线为l，焦点为F，圆M的圆心在x轴的正半轴上，圆M与y轴相切，过原点O作倾斜角为
π
3
的直线n，交直线l于点A，交圆M于不同的两点O、B，且|AO|=|BO|=2．
（1）求圆M和抛物线C的方程；
（2）若P为抛物线C上的动点，求
PM
•
PF
的最小值；
（3）过直线l上的动点Q向圆M作切线，切点分别为S、T，求证：直线ST恒过一个定点，并求该定点的坐标．
已知直线的参数方程为
x=-1+2t
y=1+
2
3
3
t
，直线l2的方程为x=3，则l1与l2的交点到点A（-1，1）的距离为
 
．
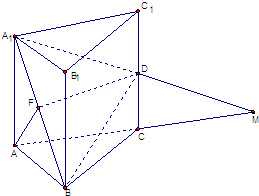已知正三棱柱A1B1C1-ABC中，AA1=AB=a，D是CC1的中点，F是A1B的中点，A1D与AC的延长线交于点M（如图），
（Ⅰ）求证：DF∥平面ABC；
（Ⅱ）求证：AF⊥BD．
已知数列{an}满足an+2=-an（n∈N*），且a1=1，a2=2，则该数列前2012项的和为（　　）
A、-3B、3C、1D、0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网