题目内容
满足|Z|=|3+4i|的复数Z在复平面上对应的点的轨迹是（ ）
分析：根据题意，设Z=x+yi，复数Z在复平面上对应的点为（x，y），计算可得|3+4i|=5，可得|Z|=5，由复数模的意义，分析可得答案．
解答：解：设Z=x+yi，复数Z在复平面上对应的点为（x，y），
由题意|Z|=|3+4i|=5，即x2+y2=25；
复数Z在复平面上对应的点的轨迹是以（0，0）为圆心，5为半径的圆．
故选：B．
由题意|Z|=|3+4i|=5，即x2+y2=25；
复数Z在复平面上对应的点的轨迹是以（0，0）为圆心，5为半径的圆．
故选：B．
点评：本题考查复数模的几何意义，关键是理解复数模的几何意义．
练习册系列答案
相关题目
已知复数z满足z-3
=-4+4i，那么复数z的模|z|等于（ ）
. |
| z |
A、
| ||
| B、5 | ||
| C、2 | ||
D、
|
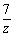∈R，又|z-1|+|z-3|=4，求复数z。