题目内容
(文科做以下(1)(2)(3))
(1)、已知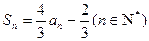 ,求数列
,求数列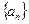 的通项公式(6分);
的通项公式(6分);
(2)、在(1)的条件下,数列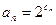 ,求证数列
,求证数列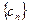 是一个 “1类和科比数列”(4分);
是一个 “1类和科比数列”(4分);
(3)、设等差数列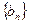 是一个 “
是一个 “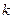 类和科比数列”,其中首项
类和科比数列”,其中首项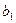 ,公差
,公差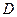 ,探究
,探究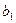
与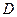 的数量关系,并写出相应的常数
的数量关系,并写出相应的常数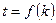 (6分);
(6分);
(1)、已知
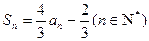 ,求数列
,求数列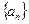 的通项公式(6分);
的通项公式(6分);(2)、在(1)的条件下,数列
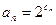 ,求证数列
,求证数列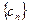 是一个 “1类和科比数列”(4分);
是一个 “1类和科比数列”(4分);(3)、设等差数列
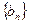 是一个 “
是一个 “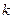 类和科比数列”,其中首项
类和科比数列”,其中首项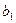 ,公差
,公差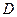 ,探究
,探究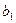
与
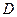 的数量关系,并写出相应的常数
的数量关系,并写出相应的常数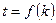 (6分);
(6分);(1)
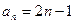
(2)略
(3)
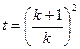
文(1)解:联立: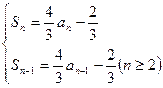
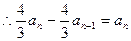 2分
2分
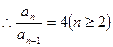 1分
1分
所以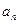 是等比数列, 1分
是等比数列, 1分
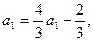
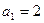 1分
1分
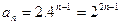 1分
1分
(2)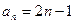 前
前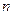 项的和
项的和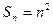 1分
1分
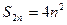 1分
1分
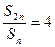 1分
1分
所以数列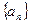 是一个 “1类和科比数列” 1分
是一个 “1类和科比数列” 1分
(3)对任意一个等差数列数列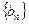 ,首项
,首项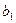 ,公差
,公差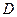
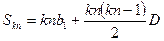 1分
1分
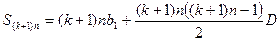 1分
1分
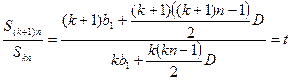 对一切
对一切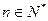 恒成立 1分
恒成立 1分
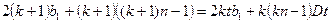 对一切
对一切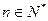 恒成立
恒成立
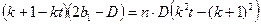 对一切
对一切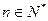 恒成立
恒成立
所以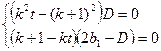 2分
2分
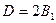 1分
1分
所以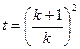 2分
2分
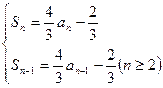
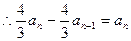 2分
2分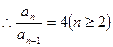 1分
1分所以
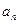 是等比数列, 1分
是等比数列, 1分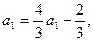
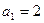 1分
1分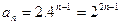 1分
1分(2)
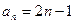 前
前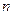 项的和
项的和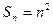 1分
1分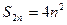 1分
1分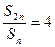 1分
1分所以数列
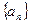 是一个 “1类和科比数列” 1分
是一个 “1类和科比数列” 1分(3)对任意一个等差数列数列
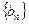 ,首项
,首项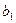 ,公差
,公差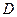
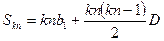 1分
1分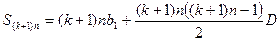 1分
1分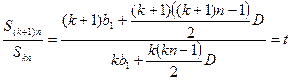 对一切
对一切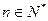 恒成立 1分
恒成立 1分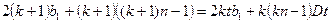 对一切
对一切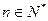 恒成立
恒成立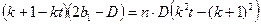 对一切
对一切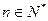 恒成立
恒成立 所以
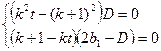 2分
2分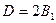 1分
1分所以
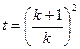 2分
2分
练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
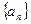 的通项公式
的通项公式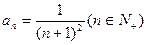 ,记
,记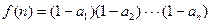 .
.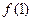 ,
,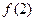 ,
,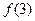 的值;
的值;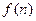 的表达式;
的表达式;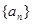 的通项公式是
的通项公式是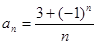 :,则
:,则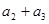 的值为
的值为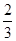
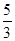
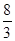
 ( )
( )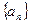 的各项都为正数,
的各项都为正数,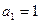 ,前
,前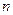 项和
项和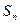 满足
满足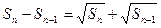 (
(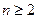 ).
).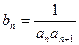 (
(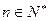 ),数列
),数列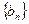 的前
的前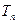 ,若
,若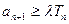 对任意正整数
对任意正整数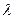 的取值范围.
的取值范围.
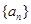 满足
满足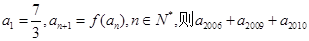 =
= 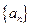 是公差不为零
是公差不为零 的等差数列,前
的等差数列,前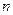 项和为
项和为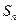 ,
,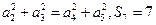 ,则使得
,则使得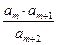 为数列
为数列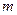 的值为
的值为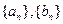 的前
的前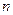 项和分别是
项和分别是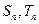 ,且
,且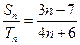 ,则
,则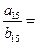
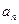 }是等差数列,
}是等差数列,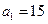 ,
, 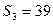 ,则过点
,则过点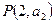 ,
,