题目内容
如图,在直角坐标系xOy中,有一组对角线长为an的正方形AnBnCnDn(n=1,2,…),其对角线BnDn依次放置在x轴上(相邻顶点重合).设{an}是首项为a,公差为d(d>0)的等差数列,点B1的坐标为(d,0).

(1)当a=8,d=4时,证明:顶点A1、A2、A3不在同一条直线上;
(2)在(1)的条件下,证明:所有顶点An均落在抛物线y2=2x上;
(3)为使所有顶点An均落在抛物线y2=2px(p>0)上,求a与d之间所应满足的关系式.
答案:
解析:
解析:
|
(2)由题意可知,顶点An的横坐标 顶点An的纵坐标 为使得所有顶点An均落在抛物线y2=2px(p>0)上,则有 又点 |

练习册系列答案
相关题目



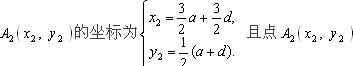 也在抛物线上,
也在抛物线上,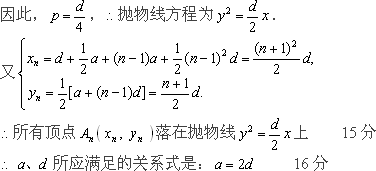
 (2009•杭州二模)如图,在直角坐标系xOy中,锐角△ABC内接于圆x2+y2=1.已知BC平行于x轴,AB所在直线方程为y=kx+m(k>0),记角A,B,C所对的边分别是a,b,c.
(2009•杭州二模)如图,在直角坐标系xOy中,锐角△ABC内接于圆x2+y2=1.已知BC平行于x轴,AB所在直线方程为y=kx+m(k>0),记角A,B,C所对的边分别是a,b,c.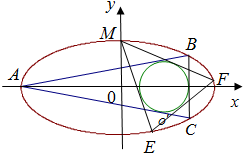 如图,在直角坐标系中,中心在原点,焦点在X轴上的椭圆G的离心率为
如图,在直角坐标系中,中心在原点,焦点在X轴上的椭圆G的离心率为 (2013•石景山区二模)如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且
(2013•石景山区二模)如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且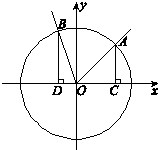 如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且
如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且 如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB: