题目内容
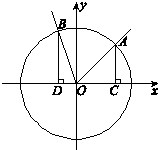 如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且α∈(
如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且α∈(| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
(Ⅰ)若x1=
| 1 |
| 4 |
(Ⅱ)分别过A,B作x轴的垂线,垂足依次为C,D.记△AOC的面积为S1,△BOD的面积为S2.若S1=S2,求角α的值.
分析:(I)根据三角函数定义求得 x1=cosα,x2=cos(α+
),再利用x1=
,求得cosα,sinα,然后利用x2=cos(α+
)=
cosα-
sinα求x2;
(II)根据图形用α的三角函数表示S1、S2,利用S1=S2求得tan2α,分析2α的范围求得2α,从而求得α.
| π |
| 6 |
| 1 |
| 4 |
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
(II)根据图形用α的三角函数表示S1、S2,利用S1=S2求得tan2α,分析2α的范围求得2α,从而求得α.
解答:解:(I)由三角函数定义,得 x1=cosα,x2=cos(α+
),
∵α∈(
,
),cosα=
,
∴sinα=
=
,
∴x2=cos(α+
)=
cosα-
sinα=
.
(Ⅱ)解:依题意得 y1=sinα,y2=sin(α+
).
∴S1=
x1y1=
sin2α,
S2=
|x2|y2=
sin(α+
)|cos(α+
)|=-
sin(2α+
),
∵S1=S2
∴sin2α=-sin(2α+
)=-
sin2α-
cos2α,
整理得tan2α=-
,
∵
<α<
,
∴
<2α<π,
∴2α=
,即α=
.
| π |
| 6 |
∵α∈(
| π |
| 3 |
| π |
| 2 |
| 1 |
| 4 |
∴sinα=
1-(
|
| ||
| 4 |
∴x2=cos(α+
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| ||||
| 8 |
(Ⅱ)解:依题意得 y1=sinα,y2=sin(α+
| π |
| 6 |
∴S1=
| 1 |
| 2 |
| 1 |
| 4 |
S2=
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 4 |
| π |
| 3 |
∵S1=S2
∴sin2α=-sin(2α+
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
整理得tan2α=-
| ||
| 3 |
∵
| π |
| 3 |
| π |
| 2 |
∴
| 2π |
| 3 |
∴2α=
| 5π |
| 6 |
| 5π |
| 12 |
点评:本题主要考查三角函数的定义及三角函数恒等变形,考查了学生运用三角函数的知识解决问题的能力.

练习册系列答案
相关题目
 (2009•杭州二模)如图,在直角坐标系xOy中,锐角△ABC内接于圆x2+y2=1.已知BC平行于x轴,AB所在直线方程为y=kx+m(k>0),记角A,B,C所对的边分别是a,b,c.
(2009•杭州二模)如图,在直角坐标系xOy中,锐角△ABC内接于圆x2+y2=1.已知BC平行于x轴,AB所在直线方程为y=kx+m(k>0),记角A,B,C所对的边分别是a,b,c.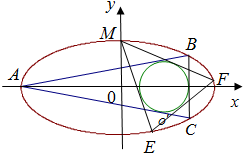 如图,在直角坐标系中,中心在原点,焦点在X轴上的椭圆G的离心率为
如图,在直角坐标系中,中心在原点,焦点在X轴上的椭圆G的离心率为 (2013•石景山区二模)如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且
(2013•石景山区二模)如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且 如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB: