题目内容
【题目】海上某货轮在A处看灯塔B在货轮的北偏东75°,距离为12![]() 海里;在A处看灯塔C在货轮的北偏西30°,距离为8
海里;在A处看灯塔C在货轮的北偏西30°,距离为8![]() 海里;货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°.(要画图)
海里;货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°.(要画图)
(1)A处与D处之间的距离;
(2)灯塔C与D处之间的距离.
【答案】解:(1)在△ABD中,∠ADB=60°,∴∠B=45°,
由正弦定理,得![]()
![]() ,
,
即AD=![]() =24(海里),
=24(海里),
(2)在△ACD中,∵AC=8![]() ,∠CAD=30°,
,∠CAD=30°,
∴由余弦定理得CD2=AD2+AC2﹣2ADACcos∠CAD=242+(8![]() )2﹣2×24×8
)2﹣2×24×8![]() cos30°=192,
cos30°=192,
解得:CD=8![]() ≈14(海里),
≈14(海里),
则灯塔C与D之间的距离约为14海里.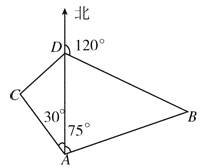
【解析】(1)在三角形ABD中,利用正弦定理列出关系式,将各自的值代入求出AD的长,即可确定出货船的航行速度;
(2)在三角形ACD中,利用余弦定理列出关系式,将各自的值代入计算即可求出CD的长.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
参考公式及数据: 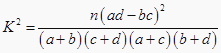
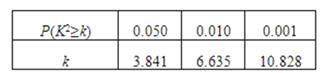
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?并说明理由?