题目内容
设 ,函数
,函数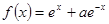 的导函数是
的导函数是 ,且
,且 是奇函数,若曲线
是奇函数,若曲线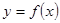 的一条切线的斜率是
的一条切线的斜率是 ,则切点的横坐标为( )
,则切点的横坐标为( )
A. | B.-ln2 | C.ln2 | D. |
C
解析试题分析:函数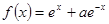 的导函数是
的导函数是 ,且
,且 是奇函数,所以
是奇函数,所以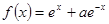 是偶函数,a=1.即
是偶函数,a=1.即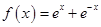 ,由切线的斜率为函数在切点的导数值,所以
,由切线的斜率为函数在切点的导数值,所以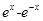 =
= ,
,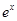 =2,x=ln2,故选C。
=2,x=ln2,故选C。
考点:本题主要考查导数的计算,导数的几何意义,函数的奇偶性。
点评:小综合题,奇函数的导数是偶函数,偶函数的导数是奇函数。切线的斜率为函数在切点的导数值。

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
设函数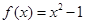 ,则
,则 在
在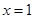 处的导数
处的导数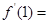 ( )
( )
A.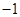 | B.0 | C.1 | D.2 |
若函数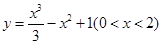 的图象上任意点处切线的倾斜角为
的图象上任意点处切线的倾斜角为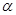 ,则
,则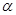 的最小值是( )
的最小值是( )
A.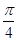 | B. | C. | D.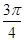 |
曲线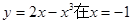 处的切线方程为( )
处的切线方程为( )
A.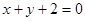 | B. |
C.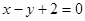 | D.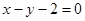 |
设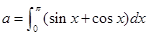 ,则二项
,则二项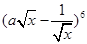 式展开式中x2项的系数是
式展开式中x2项的系数是
| A.-192 | B.193 | C.-6 | D.7 |
 ,则
,则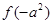 与
与 的大小关系为( )
的大小关系为( ) B.
B.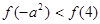
 D
D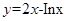 在点
在点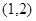 处的切线方程为( )
处的切线方程为( )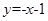 B.
B.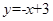 C.
C.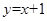 D.
D.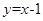
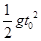
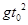
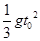
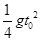
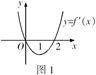
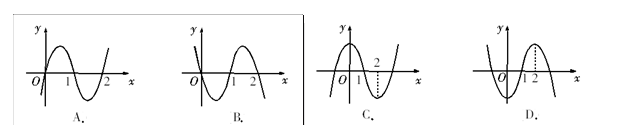
 是函数
是函数 的导函数,
的导函数, 的图象如图1所示,则
的图象如图1所示,则 的图象最有可能的是
的图象最有可能的是