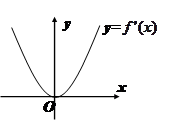题目内容
曲线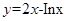 在点
在点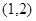 处的切线方程为( )
处的切线方程为( )
A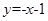 B.
B.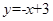 C.
C.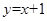 D.
D.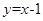
A
解析试题分析:首先确定出函数的导数,然后确定切线的斜率,利用点斜式方程得到。
解:因为曲线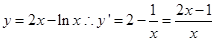 在点
在点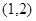 的切线斜率为1,那么由点斜式方程可知为
的切线斜率为1,那么由点斜式方程可知为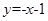 ,故选A.
,故选A.
考点:导数的几何意义
点评:解决的关键是利用导数的几何意义来分析得到求解,属于基础题。

练习册系列答案
相关题目
已知函数 的图象过原点,且在原点处的切线斜率是-3,则不等式组
的图象过原点,且在原点处的切线斜率是-3,则不等式组 所确定的平面区域在
所确定的平面区域在 内的面积为
内的面积为
A.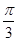 | B.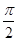 | C. | D. |
已知函数 ,则
,则 ( )
( )
| A.-1 | B.-3 | C.2 | D.-2 |
曲线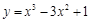 在点
在点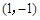 处的切线方程为
处的切线方程为
A.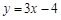 | B.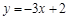 | C.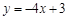 | D.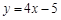 |
设 ,函数
,函数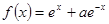 的导函数是
的导函数是 ,且
,且 是奇函数,若曲线
是奇函数,若曲线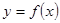 的一条切线的斜率是
的一条切线的斜率是 ,则切点的横坐标为( )
,则切点的横坐标为( )
A. | B.-ln2 | C.ln2 | D. |
曲线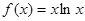 在点
在点 处的切线方程为 ( )
处的切线方程为 ( )
A. | B.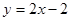 | C.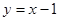 | D.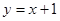 |
已知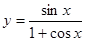 ,
,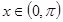 .当
.当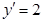 时,
时,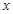 等于
等于
A.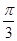 | B.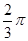 | C.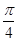 | D.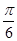 |
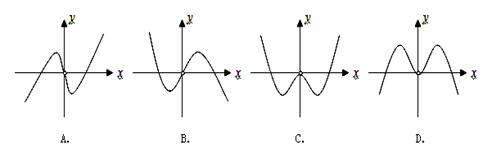
 是定义域为R的奇函数,
是定义域为R的奇函数,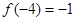 ,
,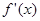 的图象如图所示。若两正数
的图象如图所示。若两正数 满足
满足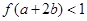 ,则
,则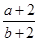 的取值范围是
的取值范围是