题目内容
曲线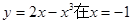 处的切线方程为( )
处的切线方程为( )
A.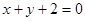 | B. |
C.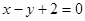 | D.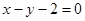 |
A.
解析试题分析:因为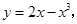 所以
所以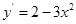 ,曲线
,曲线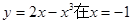 处的切线斜率为-1,x=-1,时,y=-1,故由直线方程的点斜式得曲线方程为
处的切线斜率为-1,x=-1,时,y=-1,故由直线方程的点斜式得曲线方程为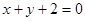 ,选A。
,选A。
考点:本题主要考查导数的几何意义,直线方程。
点评:简单题,曲线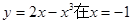 处的切线斜率,就是函数在该点的导数值。
处的切线斜率,就是函数在该点的导数值。

练习册系列答案
相关题目
已知函数 的图象过原点,且在原点处的切线斜率是-3,则不等式组
的图象过原点,且在原点处的切线斜率是-3,则不等式组 所确定的平面区域在
所确定的平面区域在 内的面积为
内的面积为
A.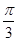 | B.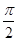 | C. | D. |
设 ,函数
,函数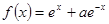 的导函数是
的导函数是 ,且
,且 是奇函数,若曲线
是奇函数,若曲线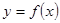 的一条切线的斜率是
的一条切线的斜率是 ,则切点的横坐标为( )
,则切点的横坐标为( )
A. | B.-ln2 | C.ln2 | D. |
曲线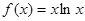 在点
在点 处的切线方程为 ( )
处的切线方程为 ( )
A. | B.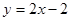 | C.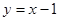 | D.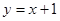 |
函数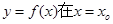 处的导数
处的导数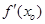 的几何意义是
的几何意义是
A.在点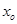 处的斜率 处的斜率 |
B.在点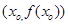 处的切线与 处的切线与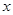 轴所夹锐角的正切值 轴所夹锐角的正切值 |
C.在点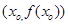 与点(0,0)连线的斜率; 与点(0,0)连线的斜率; |
D.曲线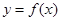 在点 在点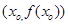 处切线的斜率 处切线的斜率 |
设函数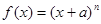 ,其中
,其中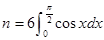 ,
, 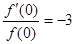 ,则
,则 的展开式中
的展开式中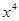 的系数为( )
的系数为( )
| A.-360 | B.360 | C.-60 | D.60 |
曲线 与坐标轴围成的面积是
与坐标轴围成的面积是
| A.4 | B. | C.3 | D.2 |
已知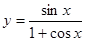 ,
,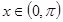 .当
.当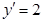 时,
时,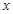 等于
等于
A.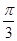 | B.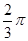 | C.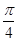 | D.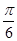 |
若点P是曲线y=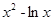 上任意一点,则点P到直线y=x-2的最小距离是 ( )
上任意一点,则点P到直线y=x-2的最小距离是 ( )
A.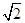 | B.1 | C.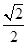 | D.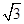 |