题目内容
【题目】已过抛物线![]() :
:![]() 的焦点
的焦点![]() 作直线
作直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,以
两点,以![]() ,
,![]() 两点为切点作抛物线的切线,两条直线交于
两点为切点作抛物线的切线,两条直线交于![]() 点.
点.
(1)当直线![]() 平行于
平行于![]() 轴时,求点
轴时,求点![]() 的坐标;
的坐标;
(2)当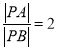 时,求直线
时,求直线![]() 的方程.
的方程.
【答案】(1)![]() ,(2)
,(2)![]()
【解析】
(1)依题![]() 的方程为
的方程为![]() ,联立抛物线方程可得
,联立抛物线方程可得![]() ,
,![]() ,利用导数求出
,利用导数求出
在![]() ,
,![]() 处的切线,再联立切线方程即可求出
处的切线,再联立切线方程即可求出![]() 点坐标.
点坐标.
(2)设![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,利用切线方程联系即可求出
,利用切线方程联系即可求出![]() .
.
法一:根据弦长公式可得,![]()
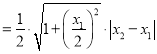 ,
, ![]()
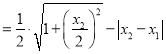 ,再根据
,再根据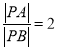
![]() ,将
,将![]() 代入即可求出结果.
代入即可求出结果.
法二:依题: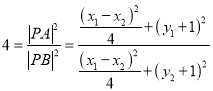 ,化简可得
,化简可得![]() ,结合
,结合![]() ,进而求出结果.得
,进而求出结果.得
(1)依题可知![]() ,当直线
,当直线![]() 平行于
平行于![]() 轴时,则
轴时,则![]() 的方程为
的方程为![]() ,
,
所以可得![]() ,
,![]() ,又
,又![]() ;
;
所以在![]() ,
,![]() 处的切线分别为:
处的切线分别为:![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
联立两切线可得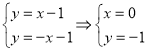 ,所以
,所以![]() .
.
(2)设![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,
,
则联立有![]() ,所以
,所以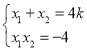 ,
,
在![]() 处的切线为:
处的切线为:![]() ,
,
同理可得,在![]() 处切线:
处切线:![]() ,
,
联立有: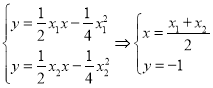 ,即点
,即点![]() .
.
法一: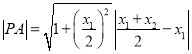
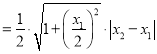 ,
,
同理可得: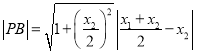
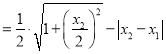 ,
,
所以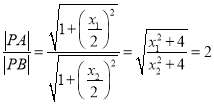
![]() ,又因为
,又因为![]() ,
,
所以解得![]() ,所以
,所以![]() ,得
,得![]() ,
,![]() 或
或![]() ,
,![]() .
.
所以直线方程为:![]() .
.
法二:
依题: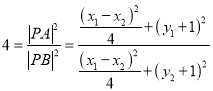
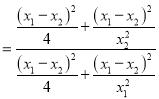 ,
,
解得![]() ,结合
,结合![]() 得
得![]() ,
,![]() 或
或![]() ,
,![]() .
.
所以直线方程为:![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】目前有声书正受着越来越多人的喜爱.某有声书公司为了解用户使用情况,随机选取了![]() 名用户,统计出年龄分布和用户付费金额(金额为整数)情况如下图.
名用户,统计出年龄分布和用户付费金额(金额为整数)情况如下图.
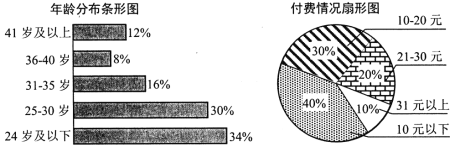
有声书公司将付费高于![]() 元的用户定义为“爱付费用户”,将年龄在
元的用户定义为“爱付费用户”,将年龄在![]() 岁及以下的用户定义为“年轻用户”.已知抽取的样本中有
岁及以下的用户定义为“年轻用户”.已知抽取的样本中有![]() 的“年轻用户”是“爱付费用户”.
的“年轻用户”是“爱付费用户”.
(1)完成下面的![]() 列联表,并据此资料,能否有
列联表,并据此资料,能否有![]() 的把握认为用户“爱付费”与其为“年轻用户”有关?
的把握认为用户“爱付费”与其为“年轻用户”有关?
爱付费用户 | 不爱付费用户 | 合计 | |
年轻用户 | |||
非年轻用户 | |||
合计 |
(2)若公司采用分层抽样方法从“爱付费用户”中随机选取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行访谈,求抽取的
人进行访谈,求抽取的![]() 人恰好都是“年轻用户”的概率.
人恰好都是“年轻用户”的概率.
|
|
|
|
|
|
|
|
|
|
|
|
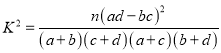 .
.
【题目】某农科站技术员为了解某品种树苗的生长情况,在该批树苗中随机抽取一个容量为100的样本,测量树苗高度(单位:![]() ).经统计,高度在区间
).经统计,高度在区间![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
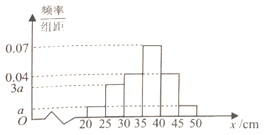
,![]() 分成6组,制成如图所示的频率分布直方图,其中高度不低于
分成6组,制成如图所示的频率分布直方图,其中高度不低于![]() 的树苗为优质树苗.
的树苗为优质树苗.
附:
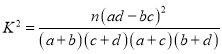 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
(1)求频率分布直方图中![]() 的值;
的值;
(2)已知所抽取的这100棵树苗来自于甲、乙两个地区,部分数据如下![]() 列联表所示,将列联表补充完整,并根据列联表判断是否有
列联表所示,将列联表补充完整,并根据列联表判断是否有![]() %的把握认为优质树苗与地区有关?
%的把握认为优质树苗与地区有关?
甲地区 | 乙地区 | 合计 | |
优质树苗 | 5 | ||
非优质树苗 | 25 | ||
合计 |
