题目内容
(本题满分14分)已知四棱锥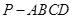 中,
中,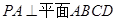 ,底面
,底面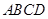 是边长为
是边长为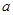 的菱形,
的菱形, ,
, .
.
(I)求证: ;
;
(II)设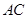 与
与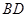 交于点
交于点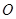 ,
,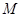 为
为 中点,若二面角
中点,若二面角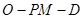 的正切值为
的正切值为 ,求
,求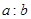 的值.
的值.

【答案】
解:(I)因为PA⊥平面ABCD,所以PA⊥BD
又ABCD为菱形,所以AC⊥BD,所以BD⊥平面PAC
从而平面PBD⊥平面PAC. ……………6分
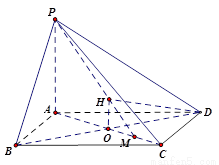
(II)过O作OH⊥PM交PM于H,连HD
因为DO⊥平面PAC,可以推出DH⊥PM,所以∠OHD为A-PM-D的平面角
又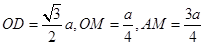 ,且
,且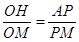
从而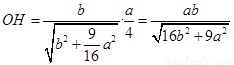
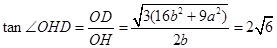
所以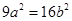 ,即
,即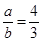 . ………………………14分
. ………………………14分
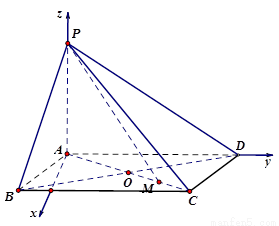
法二:如图,以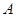 为原点,
为原点,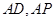 所在直线为
所在直线为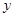 轴,
轴,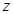 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则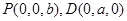 ,
,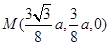 ,
, …………8分
…………8分
从而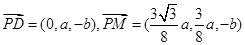
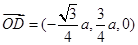
因为BD⊥平面PAC,所以平面PMO的一个法向量为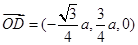 .
.
设平面PMD的法向量为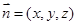 ,由
,由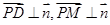 得
得
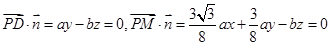
取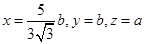 ,即
,即 ……………11分
……………11分
设 与
与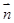 的夹角为
的夹角为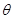 ,则二面角
,则二面角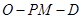 大小与
大小与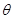 相等
相等
从而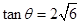 ,得
,得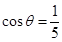
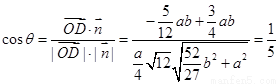
从而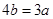 ,即
,即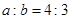 .
……………14分
.
……………14分
【解析】略

练习册系列答案
相关题目

 ,求x的值;
,求x的值; 对于
对于 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.  :
: 的离心率为
的离心率为 ,过坐标原点
,过坐标原点 且斜率为
且斜率为 的直线
的直线 与
与 、
、 ,
, .
. 、
、 的值;
的值; 与椭圆
与椭圆 的取值范围.
的取值范围. ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图). ,
,
