题目内容

若10^α=2，β=lg3，则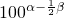 $数学公式$ =________．

$\text{[math]}$
分析：由β=lg3得10^β=3，依据有理数指数幂的运算法则将 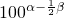$\text{[math]}$ 用10^α与10^β表示出来求值．
解答：由已知，β=lg3得10^β=3，又10^α=2，故
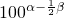$\text{[math]}$ =10^2α-β=（10^α）²÷10^β=2²÷3= $\text{[math]}$
故答案为： $\text{[math]}$
点评：本题考点是有理数指数幂的化简求值，考查根据有理数幂的去处法则将未知用已知表示出来求值．

练习册系列答案

赢在阅读限时提优训练系列答案

同步解析拓展训练系列答案

星火英语SPARK系列答案

单元检测新疆电子音像出版社系列答案

新课标数学口算天天练系列答案

恒基中考备战策略系列答案

七星图书口算速算天天练系列答案

快乐小博士小考总动员系列答案

百分阅读系列答案

初中学业考试导与练系列答案

相关题目

（附加题）
（Ⅰ）设非空集合S={x|m≤x≤l}满足：当x∈S时有x²∈S，给出下列四个结论：
①若m=2，则l=4
②若m=-

≤l≤1
③若l=

≤m≤0④若m=1，则S={1}，
其中正确的结论为

．
（Ⅱ）已知函数f(x)=x+

+b(x≠0)，其中a，b∈R．若对于任意的a∈[

，2]，f（x）≤10在x∈[

，1]上恒成立，则b的取值范围为

一个总体中100个个体的编号为0，1，2，3，…，99，并依次按编号分为10个小组，组号为0，1，2，…，9，要用系统抽样的方法抽取一个容量为10的样本，规定如果第0组（号码0～9）随机抽取的号码为l，那么依次错位地抽取后面各组的号码，即第k组中抽取的号码的个位数为l+k或l+k-10（如果l+k≥10），若l=6，则所抽取的10个号码依次是

6，17，28，39，40，51，62，73，84，95

6，17，28，39，40，51，62，73，84，95

(08年莆田四中二模文)（14分）如图，直角梯形ABCD中∠DAB＝90°，

AD∥BC，AB＝2，AD＝，BC＝．椭圆P以A、B为焦点且经过点D．

（1）建立适当坐标系，求椭圆P的方程；

（2）是否存在直线l与椭圆P交于M、N两点，且线段MN的中点为C，若存在，求l与直线AB的夹角，若不存在，说明理由．

（08年潍坊市三模文）（14分）如图，直角梯形ABCD中∠DAB＝90°，AD∥BC，AB＝2，AD＝，BC＝．椭圆C以A、B为焦点且经过点D．

　　（1）建立适当坐标系，求椭圆C的方程；

　　（2）是否存在直线l与椭圆C交于M、N两点，且线段MN的中点为C，若存在，求l与直线AB的夹角，若不存在，说明理由．

（05年浙江卷文）（14分）

如图，已知椭圆的中心在坐标原点，焦点F₁，F₂在x轴上，长轴A₁A₂的长为4，左准线l与x轴的交点为M，|MA₁|∶|A₁F₁|＝2∶1．

(Ⅰ)求椭圆的方程；

(Ⅱ)若点P为l上的动点，求∠F₁PF₂最大值．