题目内容
【题目】已知顶点为原点O的抛物线C1的焦点F与椭圆C2: ![]() =1(a>b>0)的右焦点重合,C1与C2在第一和第四象限的交点分别为A、B.
=1(a>b>0)的右焦点重合,C1与C2在第一和第四象限的交点分别为A、B.
(1)若△AOB是边长为2 ![]() 的正三角形,求抛物线C1的方程;
的正三角形,求抛物线C1的方程;
(2)若AF⊥OF,求椭圆C2的离心率e;
(3)点P为椭圆C2上的任一点,若直线AP、BP分别与x轴交于点M(m,0)和N(n,0),证明:mn=a2 .
【答案】
(1)解:设椭圆的右焦点为F(c,0),依题意得抛物线的方程为y2=4cx
∵△AOB是边长为2 ![]() 的正三角形,
的正三角形,
∴点A的坐标是 ![]() ,
,
代入抛物线的方程y2=4cx解得 ![]() ,
,
故所求抛物线C1的方程为y2=x
(2)解:∵AF⊥OF,∴点A的横坐标是c
代入椭圆方程解得 ![]() ,即点A的坐标是
,即点A的坐标是 ![]()
∵点A在抛物线y2=4cx上,
∴ ![]() ,
,
将b2=a2﹣c2代入上式整理得: ![]() ,
,
即e2+2e﹣1=0,解得 ![]()
∵0<e<1,故所求椭圆C2的离心率 ![]()
(3)证明:设P(x1,y1),A(x2,y2),B(x2,﹣y2),
代入椭圆方程得 ![]()
而直线PA的方程为(x2﹣x1)(y﹣y1)+(x﹣x1)(y1﹣y2)=0
令y=0得 ![]()
在 ![]() 中,以﹣y2代换y2得
中,以﹣y2代换y2得 ![]()
∴ ![]() =
= 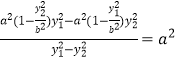
【解析】(1)确定点A的坐标是 ![]() ,代入抛物线的方程y2=4cx,求出c,即可求得抛物线C1的方程;(2)若AF⊥OF,可求A的坐标,代入抛物线的方程y2=4cx,结合b2=a2﹣c2 , 即可求椭圆C2的离心率e;(3)利用直线PA、PB的方程,令y=0得m,n的值,即可证明结论.
,代入抛物线的方程y2=4cx,求出c,即可求得抛物线C1的方程;(2)若AF⊥OF,可求A的坐标,代入抛物线的方程y2=4cx,结合b2=a2﹣c2 , 即可求椭圆C2的离心率e;(3)利用直线PA、PB的方程,令y=0得m,n的值,即可证明结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目