题目内容
设-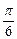 ≤x≤
≤x≤ ,求函数y=log2(1+sinx)+log2(1-sinx)的最大值和最小值.
,求函数y=log2(1+sinx)+log2(1-sinx)的最大值和最小值.
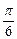 ≤x≤
≤x≤ ,求函数y=log2(1+sinx)+log2(1-sinx)的最大值和最小值.
,求函数y=log2(1+sinx)+log2(1-sinx)的最大值和最小值.在x∈[- ]上,ymax=0, ymin=-1
]上,ymax=0, ymin=-1
 ]上,ymax=0, ymin=-1
]上,ymax=0, ymin=-1 ∵在[- ]上,1+sinx>0和1-sinx>0恒成立,
]上,1+sinx>0和1-sinx>0恒成立,
∴原函数可化为y=log2(1-sin2x)=log2cos2x,
又cosx>0在[- ]上恒成立,
]上恒成立,
∴原函数即是y=2log2cosx,在x∈[- ]上,
]上,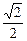 ≤cosx≤1.
≤cosx≤1.
∴log2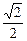 ≤log2cosx≤log21,即-1≤y≤0,也就是在x∈[-
≤log2cosx≤log21,即-1≤y≤0,也就是在x∈[- ]上,ymax=0, ymin=-1.
]上,ymax=0, ymin=-1.
 ]上,1+sinx>0和1-sinx>0恒成立,
]上,1+sinx>0和1-sinx>0恒成立,∴原函数可化为y=log2(1-sin2x)=log2cos2x,
又cosx>0在[-
 ]上恒成立,
]上恒成立,∴原函数即是y=2log2cosx,在x∈[-
 ]上,
]上,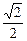 ≤cosx≤1.
≤cosx≤1.∴log2
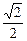 ≤log2cosx≤log21,即-1≤y≤0,也就是在x∈[-
≤log2cosx≤log21,即-1≤y≤0,也就是在x∈[- ]上,ymax=0, ymin=-1.
]上,ymax=0, ymin=-1.
练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 )在区间
)在区间 的图像如下:那么
的图像如下:那么 =( )
=( )
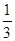


 ,将
,将 的图象向左平移
的图象向左平移 个单位后所得的图象关于
个单位后所得的图象关于 对称.(1)求实数
对称.(1)求实数 ,并求出
,并求出 上的值域.
上的值域. 图象上的一个最高点为
图象上的一个最高点为 ,由这个最高点到相邻最低点间的曲线与
,由这个最高点到相邻最低点间的曲线与 轴相交于
轴相交于 ,并写出这个函数的单调区间.
,并写出这个函数的单调区间.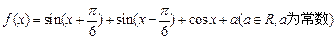 .(Ⅰ)求函数
.(Ⅰ)求函数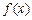 的最小正周期;(Ⅱ)若函数
的最小正周期;(Ⅱ)若函数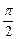 ,
,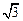 ,求实数
,求实数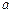 的值.
的值.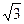 sin
sin xcos
xcos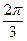 时取得最大值时的最小正整数.
时取得最大值时的最小正整数. a、b、c满足b2=ac,且边b所对的角
a、b、c满足b2=ac,且边b所对的角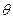 的取值集合为A,当x
的取值集合为A,当x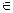 A时,求函数f(x)的值域.
A时,求函数f(x)的值域. 的图象( ).
的图象( ). 轴对称
轴对称 轴对称
轴对称 对称
对称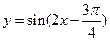 在区间
在区间 上的图像.
上的图像. ,⑴求
,⑴求 的值;⑵求
的值;⑵求 的值.
的值.