题目内容
(12分)已知函数f(x)=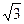 sin
sin xcos
xcos x-cos2
x-cos2 x,其中
x,其中 为使函数f(x)能在x=
为使函数f(x)能在x=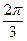 时取得最大值时的最小正整数.
时取得最大值时的最小正整数.
(1)求 的值;
的值;
(2)设△ABC的三边 a、b、c满足b2=ac,且边b所对的角
a、b、c满足b2=ac,且边b所对的角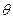 的取值集合为A,当x
的取值集合为A,当x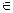 A时,求函数f(x)的值域.
A时,求函数f(x)的值域.
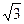 sin
sin xcos
xcos x-cos2
x-cos2 x,其中
x,其中 为使函数f(x)能在x=
为使函数f(x)能在x=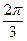 时取得最大值时的最小正整数.
时取得最大值时的最小正整数.(1)求
 的值;
的值;(2)设△ABC的三边
 a、b、c满足b2=ac,且边b所对的角
a、b、c满足b2=ac,且边b所对的角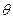 的取值集合为A,当x
的取值集合为A,当x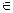 A时,求函数f(x)的值域.
A时,求函数f(x)的值域.(1)2 (2)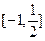
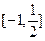
由于f(x)=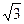 sin
sin xcos
xcos x-cos2
x-cos2 x=
x=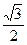 sin2
sin2 x-
x-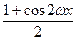
=sin(2 x-
x-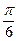 )-
)-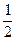 ,
,
(1)由题意可知,2 ·
·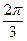
 -
-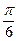 =
=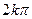 +
+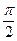 ,即
,即 =
=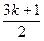 (k
(k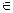 Z),
Z),
所以当k=1时, =2即为所求;
=2即为所求;
(2)由余弦定理得cos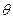 =
=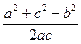 =
=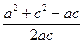
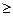
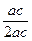 =
=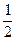 (当a=c时取“=”),
(当a=c时取“=”),
所以0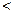
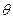
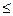
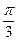 ,即A={
,即A={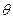 |0
|0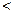
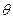
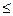
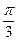 }.又由(1)知,f(x)= sin(4x-
}.又由(1)知,f(x)= sin(4x-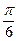 )-
)-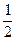 ,
,
由x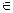 A得0
A得0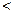 x
x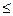
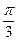 ,即-
,即-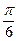
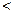 4x-
4x-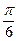
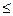
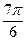 ,
,
所以-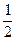
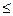 sin(4x-
sin(4x-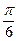 )
)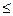 1,故函数f(x)的值域
1,故函数f(x)的值域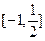 .
.
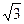 sin
sin xcos
xcos x-cos2
x-cos2 x=
x=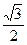 sin2
sin2 x-
x-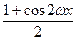
=sin(2
 x-
x-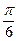 )-
)-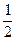 ,
,(1)由题意可知,2
 ·
·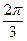
 -
-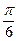 =
=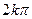 +
+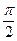 ,即
,即 =
=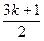 (k
(k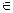 Z),
Z),所以当k=1时,
 =2即为所求;
=2即为所求;(2)由余弦定理得cos
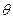 =
=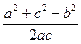 =
=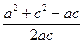
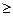
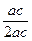 =
=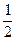 (当a=c时取“=”),
(当a=c时取“=”),所以0
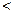
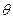
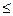
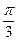 ,即A={
,即A={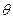 |0
|0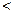
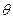
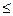
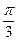 }.又由(1)知,f(x)= sin(4x-
}.又由(1)知,f(x)= sin(4x-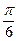 )-
)-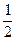 ,
, 由x
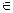 A得0
A得0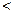 x
x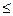
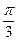 ,即-
,即-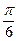
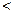 4x-
4x-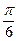
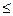
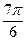 ,
,所以-
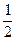
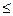 sin(4x-
sin(4x-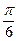 )
)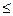 1,故函数f(x)的值域
1,故函数f(x)的值域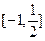 .
.
练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 (米)随着时间
(米)随着时间 而周期性变化,每天各时刻
而周期性变化,每天各时刻 的浪高数据的平均值如下表:
的浪高数据的平均值如下表:

 中选择一个合适的函数模型,并求出该拟合模型的解析式;
中选择一个合适的函数模型,并求出该拟合模型的解析式; (其中
(其中 )的图象与x轴在原点右侧的第一个交点为N(6,0),又
)的图象与x轴在原点右侧的第一个交点为N(6,0),又 (1)求这个函数解析式(2)设关于x的方程
(1)求这个函数解析式(2)设关于x的方程 在[0,8]内有两个不同根
在[0,8]内有两个不同根 ,求
,求 的值及k的取值范围。
的值及k的取值范围。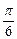 ≤x≤
≤x≤ ,求函数y=log2(1+sinx)+log2(1-sinx)的最大值和最小值.
,求函数y=log2(1+sinx)+log2(1-sinx)的最大值和最小值. 的图象先向左平移
的图象先向左平移 个单位,然后向上平移1个单位,得到函数
个单位,然后向上平移1个单位,得到函数 的图象,则
的图象,则 是( )
是( ) 
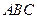 中,内角
中,内角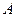 、
、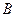 、
、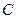 所对的边分别是
所对的边分别是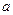 、
、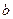 、
、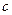 ,已知
,已知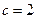 ,
,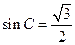 ,(1)若
,(1)若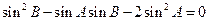 ,求
,求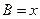 ,△
,△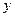 ,试求函数
,试求函数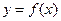 的最大值.
的最大值. 的最小正周期和最大值分别为 .
的最小正周期和最大值分别为 . 的图象中相邻的两条对称轴间距离为 ( )
的图象中相邻的两条对称轴间距离为 ( ) 


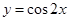 的图象,只需将函数
的图象,只需将函数 的图象( )
的图象( ) B、向右平移
B、向右平移 D、向右平移
D、向右平移