题目内容
已知函数 ,且
,且 在
在 和
和 处取得极值.
处取得极值.
(1)求函数 的解析式.
的解析式.
(2)设函数 ,是否存在实数
,是否存在实数 ,使得曲线
,使得曲线 与
与 轴有两个交点,若存在,求出
轴有两个交点,若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】
(1)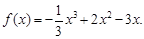
(2)存在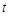 ,且
,且 或
或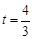 时,使得曲线
时,使得曲线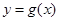 与
与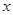 轴有两个交
轴有两个交
【解析】
试题分析:解:(1)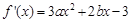 ,
,
因为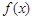 在
在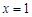 和
和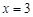 处取得极值,
处取得极值,
所以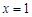 和
和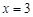 是
是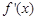 =0的两个根,
=0的两个根,
则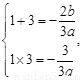 解得
解得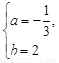 经检验符合已知条件
经检验符合已知条件
故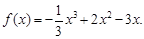
(2)由题意知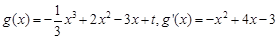 ,
,
令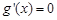 得,
得,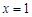 或
或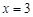 ,
,
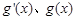 随着
随着 变化情况如下表所示:
变化情况如下表所示:
|
|
|
1 |
(1,3) |
3 |
|
|
|
- |
0 |
+ |
0 |
- |
|
|
递减 |
极小值 |
递增 |
极大值 |
递减 |
由上表可知: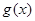 极大值=
极大值=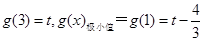 ,
,
又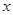 取足够大的正数时,
取足够大的正数时,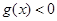 ;
;
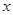 取足够小的负数时,
取足够小的负数时,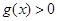 ,
,
因此,为使曲线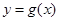 与
与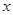 轴有两个交点,结合
轴有两个交点,结合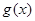 的单调性,
的单调性,
得: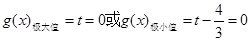 ,
,
∴ 或
或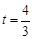 ,
,
即存在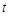 ,且
,且 或
或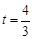 时,使得曲线
时,使得曲线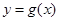 与
与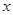 轴有两个交点.
轴有两个交点.
考点:导数的运用
点评:根据导数的符号判定函数的单调性是解题的关键,同时能利用其极值于x轴的关系的求解交点问题,属于中档题。

练习册系列答案
相关题目
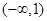
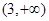
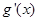
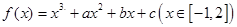 ,且函数
,且函数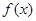 在
在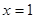 和
和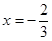 处都取得极值。
处都取得极值。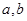 的值;
的值;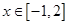 ,
,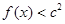 恒成立,求实数
恒成立,求实数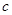 的取值范围。
的取值范围。 和图象过坐标原点O,且在点(-1,f(-1))处的切线的斜率是-5。
和图象过坐标原点O,且在点(-1,f(-1))处的切线的斜率是-5。 的图象经过点
的图象经过点 、
、 与点
与点 ,设函数
,设函数 在
在 和
和 处取到极值,其中
处取到极值,其中 ,
, 。
。 的二次项系数
的二次项系数 的值;
的值; 的大小(要求按从小到大排列);
的大小(要求按从小到大排列); ,且过原点存在两条互相垂直的直线与曲线
,且过原点存在两条互相垂直的直线与曲线 均相切,求
均相切,求