题目内容
已知函数![]() .
.
⑴若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() 和
和![]() 的值;
的值;
⑵求证;![]() 对任意
对任意![]() 恒成立的充要条件是
恒成立的充要条件是![]() ;
;
⑶若![]() ,且对任意
,且对任意![]() 、
、![]() ,都
,都![]() ,求
,求![]() 的取值范围.
的取值范围.
解:⑴![]() ,
,![]() ,又
,又![]() ,所以曲线
,所以曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() 即
即![]() ,
,
由已知得![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
⑵充分性
当![]() 时,
时,![]() ,
,![]()
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
![]() ;
;
必要性
![]()
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是减函数,而
上是减函数,而![]() ,
,
故![]() 时,
时,![]() ,与
,与![]() 恒成立矛盾,所以
恒成立矛盾,所以![]() 不成立
不成立
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
![]() ;
;
因为![]() ,又当
,又当![]() 时,
时,![]() ,
,![]() 与
与![]() 恒成立不符.
恒成立不符.
所以![]() .
.
综上,![]() 对任意
对任意![]() 恒成立的充要条件是
恒成立的充要条件是![]() ;
;
⑶当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上是减函数,
上是减函数,
不妨设且![]()
![]()
![]()
![]() ,则
,则![]() ,
,![]() ,
,
∴![]() 等价于
等价于![]() ,即
,即![]()
令![]() ,
,![]() 在
在![]() 上是减函数,
上是减函数,
∵![]() ,
,
∴![]() 在
在![]() 时恒成立,
时恒成立,
∴![]() ,
,![]() ,又
,又![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]()

练习册系列答案
相关题目
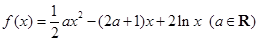 .
. 在
在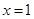 和
和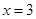 处的切线互相平行,求
处的切线互相平行,求 的值;
的值;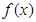 的单调区间;
的单调区间;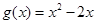 ,若对任意
,若对任意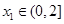 ,均存在
,均存在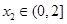 ,使得
,使得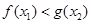 ,求
,求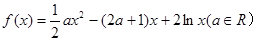
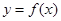 在
在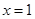 和
和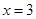 处的切线互相平行,求
处的切线互相平行,求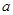 的值及函数
的值及函数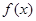 的单调区间;
的单调区间;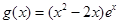 ,若对任意
,若对任意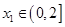 ,均存在
,均存在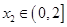 ,使得
,使得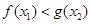 ,求实数
,求实数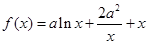 .
.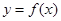 在点
在点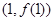 处的切线与直线
处的切线与直线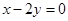 垂直,求实数
垂直,求实数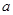 的值.
的值.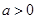 ,求
,求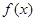 的最小值
的最小值 ;
;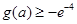 .
.
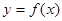 在
在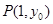 处的切线平行于直线
处的切线平行于直线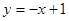 ,求函数
,求函数 ,且对
,且对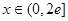 时,
时,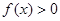 恒成立,求实数
恒成立,求实数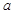 的取值范围.
的取值范围.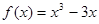 ,若曲线
,若曲线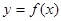 在点A(0,16)处的切线方程为
在点A(0,16)处的切线方程为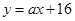 ,则实数
,则实数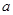 的值是( )
的值是( )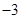 B.
B.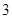 C.6
D.9
C.6
D.9