题目内容
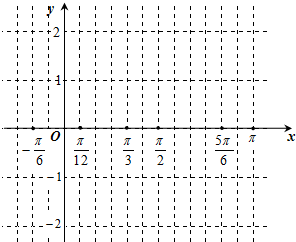已知函数f(x)=sin(2x+| π |
| 3 |
（Ⅰ）在给定的坐标系内，用“五点作图法”列表画出函数y=f（x）在一个周期内的图象；
（Ⅱ）如何由函数f（x）的图象通过适当的变换得到函数y=sinx的图象，写出变换过程．
（Ⅲ）若f(x)=-
| 3 |
| 5 |
| π |
| 2 |
分析：（Ⅰ）直接利用五点法，令2x+
=0，
，π，
，2π，求出对应的x即可找到五个特殊点的坐标，即可得到函数图象．
（Ⅱ）直接根据函数图象的平移变换和伸缩变换规律即可得到；
（Ⅲ）先根据已知条件求出cos（2x+
）的值，在利用两角差的余弦公式即可求出结论．
| π |
| 3 |
| π |
| 2 |
| 3π |
| 2 |
（Ⅱ）直接根据函数图象的平移变换和伸缩变换规律即可得到；
（Ⅲ）先根据已知条件求出cos（2x+
| π |
| 3 |
解答：解：（Ⅰ）令2x+
=0，
，π，
，2π，
解得：x=-
，
，
，
，
．
所以函数f(x)=sin(2x+
)过点（-
，0）（
，1），（
，0），（
，-1），（
，0）．
在题中所给的坐标系中把这五个点用光滑的曲线连起来即可．
（Ⅱ）函数f（x）=sin（2x+
）的图象上各点的纵坐标不变，横坐标伸长到原来的2倍得到f（x）=sin（x+
），在整体相右平移
个单位即可得到f（x）=sinx．
（Ⅲ）∵x∈（0，
），
∴2x+
∈（
，
），
又因为f（x）=sin（2x+
）=-
＜0．
∴cos（2x+
）=-
=-
．
∴sin2x=sin[（2x+
）-
]
=sin（2x+
）•cos
-cos（2x+
）•sin
=（-
）×
-（-
）×
=
．
| π |
| 3 |
| π |
| 2 |
| 3π |
| 2 |
解得：x=-
| π |
| 6 |
| π |
| 12 |
| π |
| 3 |
| 7π |
| 12 |
| 5π |
| 6 |
所以函数f(x)=sin(2x+
| π |
| 3 |
| π |
| 6 |
| π |
| 12 |
| π |
| 3 |
| 7π |
| 12 |
| 5π |
| 6 |
在题中所给的坐标系中把这五个点用光滑的曲线连起来即可．
（Ⅱ）函数f（x）=sin（2x+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
（Ⅲ）∵x∈（0，
| π |
| 2 |
∴2x+
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
又因为f（x）=sin（2x+
| π |
| 3 |
| 3 |
| 5 |
∴cos（2x+
| π |
| 3 |
1-sin 2(2x+
|
| 4 |
| 5 |
∴sin2x=sin[（2x+
| π |
| 3 |
| π |
| 3 |
=sin（2x+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
=（-
| 3 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
| ||
| 2 |
=
4
| ||
| 10 |
点评：本题主要考查三角函数的平移．三角函数的平移原则为左加右减上加下减．注意分清哪个是平移前的函数，哪个是平移后的函数．
练习册系列答案
相关题目
将正奇数列{2n-1}中的所有项按每一行比上一行多一项的规则排成如下数表：