题目内容
8.解不等式:x2-x+a-a2<0.分析 原不等式等价转化为[x+(a-1)](x-a)<0,由a的取值范围分类讨论,由此能求出原不等式的解集.
解答 解:∵x2-x+a-a2<0,
∴x2-x-a(a-1)<0,
∴[x+(a-1)](x-a)<0
∴当-(a-1)>a时,即a<$\frac{1}{2}$时,
不等式:x2-x+a-a2<0的解集是{x|a<x<1-a};
当-(a-1)=a时,即a=$\frac{1}{2}$,
(x-$\frac{1}{2}$)2<0不存在,
不等式:x2-x+a-a2<0的解集是∅;
当-(a-1)<a时,即a>$\frac{1}{2}$时,
不等式:x2-x+a-a2<0的解集是{x|1-a<x<a}.
点评 本题考查含参一元二次不等式的解法,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.如图,在复平面内,复数z1和z2对应的点分别是A和B,则$\frac{{z}_{2}}{{z}_{1}}$=( )
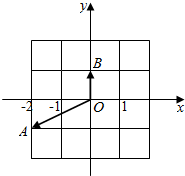

| A. | $\frac{1}{5}$+$\frac{2}{5}$i | B. | $\frac{2}{5}$+$\frac{1}{5}$i | C. | -$\frac{1}{5}$-$\frac{2}{5}$i | D. | -$\frac{2}{5}$-$\frac{1}{5}$i |
19.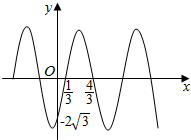 已知函数f(x)=Asin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示,则下列判断错误的是( )
已知函数f(x)=Asin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示,则下列判断错误的是( )
 已知函数f(x)=Asin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示,则下列判断错误的是( )
已知函数f(x)=Asin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示,则下列判断错误的是( )| A. | 函数f(x)的最小正周期为2 | |
| B. | 函数f(x)的值域为[一4,4] | |
| C. | 函数f(x)的图象关于( $\frac{10}{3}$,0)对称 | |
| D. | 函数f(x)的图象向左平移 $\frac{π}{3}$个单位后得到y=Asinωx的图象 |
20.下列各对向量中,共线的是( )
| A. | $\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(3,-2) | B. | $\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(4,-6) | C. | $\overrightarrow{a}$=(1,$\sqrt{3}$),$\overrightarrow{b}$=($\sqrt{3}$,3) | D. | $\overrightarrow{a}$=(4,7),$\overrightarrow{b}$=(7,4) |
17.零向量的方向规定为( )
| A. | 向左 | B. | 向右 | C. | 坐标轴方向 | D. | 不确定 |
18.设点P在曲线y=2ex上,点Q在曲线y=lnx-ln2上,则|PQ|的最小值为( )
| A. | 1-ln2 | B. | $\sqrt{2}$(1-ln2) | C. | 2(1+ln2) | D. | $\sqrt{2}$(1+ln2) |