题目内容
如图，矩形ABCD中，DC=
，AD=1，在DC上截取DE=1，将△ADE沿AE翻折到D1点，点D1在平面ABC上的射影落在AC上时，二面角D1-AE-B的平面角的余弦值是 ．
【答案】分析：过D1作D1F⊥AE于F，连接GF，由三垂线定理可得∠D1FG即为二面角D1-AE-B的平面角的平面角，角三角形D1FG，即可得到答案．
解答：
解：令点D1在平面ABC上的射影为G，过D1作D1F⊥AE于F，连接GF
则∠D1FG即为二面角D1-AE-B的平面角的平面角
又∵DC=
，AD=1，DE=1，
∴D1F=AF=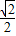
，∠FAG=15°，则FG=
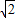-1
则cos∠D1FG=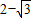
故答案为：
点评：本题考查的知识点是二面角的平面角及求法，其中根据确定出二面角的平面角是解答本题的关键．
解答：
解：令点D1在平面ABC上的射影为G，过D1作D1F⊥AE于F，连接GF则∠D1FG即为二面角D1-AE-B的平面角的平面角
又∵DC=
，AD=1，DE=1，∴D1F=AF=
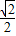，∠FAG=15°，则FG=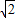-1则cos∠D1FG=
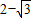
故答案为：
点评：本题考查的知识点是二面角的平面角及求法，其中根据确定出二面角的平面角是解答本题的关键．
练习册系列答案
应用题作业本系列答案
相关题目
如图，矩形ABCD中，AB=
A 若方程ax-x-a=0有两个实数解，则a的取值范围是
如图，矩形ABCD中，
（理）如图，矩形ABCD中，AB=1，BC=a，PA⊥平面ABCD