题目内容
 如图,矩形ABCD中,AB=
如图,矩形ABCD中,AB=8
| ||
| 3 |
(I)建立适当的平面直角坐标系,求椭圆M的方程;
(II)过椭圆M的中心作直线l与椭圆交于P,Q两点,设椭圆的右焦点为F2,当∠PF2Q=
| 2π |
| 3 |
分析:先以过O平行于AB的直线为x轴,以过O平行于AD的直线为y轴建立直角坐标系.
(1)设椭圆方程为
+
=1,根据题目中准线方程、短轴长和离心率确定a,b,c的值,代入即可确定方程.
(2)先求出|PF1|、|PF2|的距离,根据对称性可知|PF1|=|QF2|,再由三角形面积公式可得到答案.
(1)设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
(2)先求出|PF1|、|PF2|的距离,根据对称性可知|PF1|=|QF2|,再由三角形面积公式可得到答案.
解答: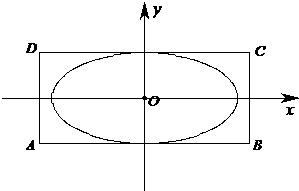 解;如图,建立直角坐标系,
解;如图,建立直角坐标系,
依题意:设椭圆方程为
+
=1(a>b>0),
(I)依题意:
=
,b=1,a2=b2+c2,
∵椭圆M的离心率大于0.7,所以a2=4,b2=1.
∴椭圆方程为
+y2=1.
(II)因为直线l过原点与椭圆交于点P,Q,
设椭圆M的左焦点为F1.
由对称性可知,四边形PF1QF2是平行四边形.
∴△PF2Q的面积等于△PF1F2的面积.
∵∠PF2Q=
,
∴∠F1PF2=
.
设|PF1|=r1,|PF2|=r2,
则
∴r1r2=
.
∴S△PF2Q=S△F2PF1=
r1r2sin
=
.
 解;如图,建立直角坐标系,
解;如图,建立直角坐标系,依题意:设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
(I)依题意:
| a2 |
| c |
4
| ||
| 3 |
∵椭圆M的离心率大于0.7,所以a2=4,b2=1.
∴椭圆方程为
| x2 |
| 4 |
(II)因为直线l过原点与椭圆交于点P,Q,
设椭圆M的左焦点为F1.
由对称性可知,四边形PF1QF2是平行四边形.
∴△PF2Q的面积等于△PF1F2的面积.
∵∠PF2Q=
| 2π |
| 3 |
∴∠F1PF2=
| π |
| 3 |
设|PF1|=r1,|PF2|=r2,
则
|
∴r1r2=
| 4 |
| 3 |
∴S△PF2Q=S△F2PF1=
| 1 |
| 2 |
| π |
| 3 |
| ||
| 3 |
点评:本题主要考查椭圆的标准方程.圆锥曲线是每年必考题,对于圆锥曲线的基础知识一定要熟练掌握.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目

 A 若方程ax-x-a=0有两个实数解,则a的取值范围是
A 若方程ax-x-a=0有两个实数解,则a的取值范围是 如图,矩形ABCD中,
如图,矩形ABCD中, (理)如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD
(理)如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD