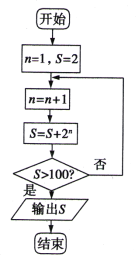
��Ŀ����
����Ŀ��Ϊ�˻�������ӵ�µĽ�ͨ״�������ٳ���ʵʩ���ƾ��۲��ԣ��Կ��Ƴ�������.ij�س��ƾ��۵Ļ��������ǣ��١�ä�ġ��������в��뾺�ĵ��˶�Ҫ���籨��һ�Σ�ÿ���˲�֪�������˵ı��ۣ�Ҳ��֪�����뵱�ھ��ĵ����������ھ���ʱ���ֹ��ϵͳ���ݵ��ڳ��������վ����˵ij��۴Ӹߵ��ͷ�������.ij����μ�![]() ��
��![]() �·ݵij��ƾ��ģ���Ϊ��Ԥ����ͳɽ��ۣ����ݾ�����վ�����ݣ�ͳ�������
�·ݵij��ƾ��ģ���Ϊ��Ԥ����ͳɽ��ۣ����ݾ�����վ�����ݣ�ͳ�������![]() ���²��뾺�ĵ����������±�����
���²��뾺�ĵ����������±�����
�·� |
|
|
|
|
|
�·ݱ�� |
|
|
|
|
|
�������� |
|
|
|
|
|
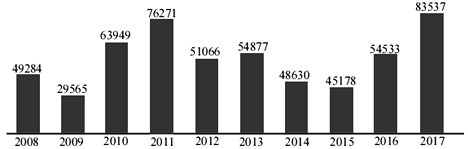
��1�����ռ����ݵ�ɢ��ͼ���֣��������Իع�ģ����Ͼ�������![]() �����ˣ����·ݱ��
�����ˣ����·ݱ��![]() ֮�����ع�ϵ.������С���˷���
֮�����ع�ϵ.������С���˷���![]() ����
����![]() �����Իع鷽�̣�
�����Իع鷽�̣�![]() ����Ԥ��
����Ԥ��![]() ��
��![]() �·ݲ��뾺�ĵ�����.
�·ݲ��뾺�ĵ�����.
��2��ij�г����л�������μ�![]() ��
��![]() �·ݳ��ƾ�����Ա�У������ȡ��
�·ݳ��ƾ�����Ա�У������ȡ��![]() �ˣ������ǵ��ⱨ�ۼ۸�����˵��飬�õ�����Ƶ���ֲ�����Ƶ�ʷֲ�ֱ��ͼ��
�ˣ������ǵ��ⱨ�ۼ۸�����˵��飬�õ�����Ƶ���ֲ�����Ƶ�ʷֲ�ֱ��ͼ��
�������䣨��Ԫ�� |
|
|
|
|
|
|
|
Ƶ�� |
|
|
|
|
|
|
|
��i����![]() ��
��![]() ��ֵ����
��ֵ����![]() λ������Ա�б��۴���
λ������Ա�б��۴���![]() ��Ԫ�ĸ��ʣ�
��Ԫ�ĸ��ʣ�
��ii����![]() ��
��![]() �·ݳ����������Ϊ
�·ݳ����������Ϊ![]() �����辺�ı����ڸ�����ֲ��Ǿ��ȵģ�����������ϳ�����������Ϣ��Ԥ�⣨��˵�����ɣ����ĵ���ͳɽ���.
�����辺�ı����ڸ�����ֲ��Ǿ��ȵģ�����������ϳ�����������Ϣ��Ԥ�⣨��˵�����ɣ����ĵ���ͳɽ���.
�ο���ʽ�����ݣ��ٻع鷽��![]() ������
������ ��
��![]() ��
��
��![]() ��
��![]() .
.

���𰸡���1��2018��5�·ݲ��뾺�ĵ���������Ϊ2���ˣ���2����![]()
����Ϊ![]() ����ͳɽ���Ϊ
����ͳɽ���Ϊ![]() ��Ԫ..
��Ԫ..
��������������(1)�����ֵ![]() ��
��![]() �����빫ʽ��
�����빫ʽ��![]() ���ٸ���
���ٸ���![]() ��
��![]() �����������Իع鷽����Ԥ��ֵ��(2) �ٸ���Ƶ������������Ƶ�ʵij˻���a������Ƶ�ʷֲ�ֱ��ͼ������С�����������Ϊ1��b���ٸ���Ƶ�ʵ���Ƶ�����������ý��������������ͳɽ�����������ռ�������������ٶ�ӦƵ�ʷֲ�ֱ��ͼƵ�ʣ�ȷ�����.
�����������Իع鷽����Ԥ��ֵ��(2) �ٸ���Ƶ������������Ƶ�ʵij˻���a������Ƶ�ʷֲ�ֱ��ͼ������С�����������Ϊ1��b���ٸ���Ƶ�ʵ���Ƶ�����������ý��������������ͳɽ�����������ռ�������������ٶ�ӦƵ�ʷֲ�ֱ��ͼƵ�ʣ�ȷ�����.
��⣺��1����֪![]() ��
��![]() ��
��
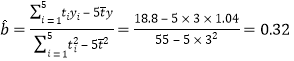 ��
��
![]() ��
��
��![]() ����
����![]() �����Իع鷽��Ϊ
�����Իع鷽��Ϊ![]() ��
��
��![]() ʱ,
ʱ,![]() ����2018��5�·ݲ��뾺�ĵ���������Ϊ2����.
����2018��5�·ݲ��뾺�ĵ���������Ϊ2����.
��2����i����![]() ���
���![]() ��
��
��Ƶ�ʺ�Ϊ1����![]() �����
�����![]() ��
��
![]() λ������Ա���۴���5��Ԫ������Ϊ
λ������Ա���۴���5��Ԫ������Ϊ![]() �ˣ�
�ˣ�
��![]() λ������Ա�б��۴���
λ������Ա�б��۴���![]() ��Ԫ�ĸ���Ϊ
��Ԫ�ĸ���Ϊ![]()
��ii��2018��5�·�ʵ�ʷ��ų�������Ϊ3000�����ݾ��۹���������ͳɽ�����������ռ����������Ϊ![]() ������Ƶ�ʷֲ�ֱ��ͼ֪���ı��۴���6��Ԫ��Ƶ��Ϊ
������Ƶ�ʷֲ�ֱ��ͼ֪���ı��۴���6��Ԫ��Ƶ��Ϊ![]() ��
��
���ԣ�����ͳ��˼�루�����������壩��Ԥ��2018��5�·ݾ��ĵ���ͳɽ���Ϊ![]() ��Ԫ.
��Ԫ.