题目内容
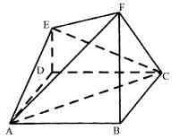 如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.
如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.(1)求点E到平面FBC的距离;
(2)求证:平面AEC⊥平面AFC.
分析:(1)由题意可得:DE∥BF,所以DE∥平面BFC,故点D到平面BFC的距离等于点E到平面BFC的距离.由题意可得DC⊥平面BFC,所以DC即为点D到平面BFC的距离,进而得到答案.
(2)连接BD交AC于O,连接OE、OF,所以AE=EC并且EO⊥AC.又因为在△EOF中,EO=
=
,OF=
=
,EF=3,所以OE⊥OF.又因为OE⊥AC,所以EO⊥平面AFC,根据面面垂直的判定定理即可得到面面垂直.
(2)连接BD交AC于O,连接OE、OF,所以AE=EC并且EO⊥AC.又因为在△EOF中,EO=
| 2+1 |
| 3 |
| 2+4 |
| 6 |
解答:解:(1)由题意可得:DE⊥平面ABCD,BF⊥平面ABCD,
所以DE∥BF,
又因为DE?平面BFC,BF?平面BFC,
所以DE∥平面BFC,
故点D到平面BFC的距离等于点E到平面BFC的距离.
因为BF⊥平面ABCD,并且正方形ABCD中,DC⊥BC,
所以DC⊥平面BFC,
所以DC即为点D到平面BFC的距离,
所以点E到平面BFC的距离为2.
(2)连接BD交AC于O,连接OE、OF,
因为DE⊥平面ABCD,AD=DC,
所以AE=EC.
又因为O为AC的中点,
所以EO⊥AC.
又因为在△EOF中,EO=
=
,OF=
=
,EF=3,
所以OE⊥OF.
又因为OE⊥AC,所以EO⊥平面AFC.
又因为OE?平面ACE,
所以平面AEC⊥平面AFC.
所以DE∥BF,
又因为DE?平面BFC,BF?平面BFC,
所以DE∥平面BFC,
故点D到平面BFC的距离等于点E到平面BFC的距离.
因为BF⊥平面ABCD,并且正方形ABCD中,DC⊥BC,
所以DC⊥平面BFC,
所以DC即为点D到平面BFC的距离,
所以点E到平面BFC的距离为2.
(2)连接BD交AC于O,连接OE、OF,
因为DE⊥平面ABCD,AD=DC,
所以AE=EC.
又因为O为AC的中点,
所以EO⊥AC.
又因为在△EOF中,EO=
| 2+1 |
| 3 |
| 2+4 |
| 6 |
所以OE⊥OF.
又因为OE⊥AC,所以EO⊥平面AFC.
又因为OE?平面ACE,
所以平面AEC⊥平面AFC.
点评:解决此类问题的关键是熟练掌握几何体的结构特征以及熟练掌握有关线面位置关系的定理.

练习册系列答案
相关题目
 如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a.
如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a. 如图,已知ABCD是底角为30°的等腰梯形,AD=2
如图,已知ABCD是底角为30°的等腰梯形,AD=2 如图,已知ABCD是边长为1的正方形,AF⊥平面ABCD,CE∥AF,CE=λAF(λ>1).
如图,已知ABCD是边长为1的正方形,AF⊥平面ABCD,CE∥AF,CE=λAF(λ>1). 如图,已知ABCD是矩形,PD⊥平面ABCD,PB=2,PB与平面ABCD所成的角为30°,PB与平面PCD所成的角为45°,求:
如图,已知ABCD是矩形,PD⊥平面ABCD,PB=2,PB与平面ABCD所成的角为30°,PB与平面PCD所成的角为45°,求: 如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE.
如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE.