题目内容
 如图,已知ABCD是边长为1的正方形,AF⊥平面ABCD,CE∥AF,CE=λAF(λ>1).
如图,已知ABCD是边长为1的正方形,AF⊥平面ABCD,CE∥AF,CE=λAF(λ>1).(Ⅰ)证明:BD⊥EF;
(Ⅱ)若AF=1,且直线BE与平面ACE所成角的正弦值为
3
| ||
| 10 |
分析:(I)方法1(几何法):连接BD、AC,交点为O,由正方形的性质得BD⊥AC,由线面垂直的性质,可得AF⊥BD,进而由线面垂直的判定定理得到BD⊥平面ACEF,进而BD⊥EF;
(I)方法2(向量法):建立空间直角坐标系A-xyz,分别求出BD和EF的方向向量,进而根据两个向量的数量积为0,可得BD⊥EF;
(Ⅱ)方法1:连接OE,由(Ⅰ)方法1知,BD⊥平面ACEF,所以∠BEO即为直线BE与平面ACE所成的角,解Rt△BEO可得λ值.
(Ⅱ)方法2:由
=(0,1,λ),
=(-1,1,0)是平面ACE的法向量.则直线BE与面ACE所成角为θ满足sinθ=
,代入可得λ值.
(I)方法2(向量法):建立空间直角坐标系A-xyz,分别求出BD和EF的方向向量,进而根据两个向量的数量积为0,可得BD⊥EF;
(Ⅱ)方法1:连接OE,由(Ⅰ)方法1知,BD⊥平面ACEF,所以∠BEO即为直线BE与平面ACE所成的角,解Rt△BEO可得λ值.
(Ⅱ)方法2:由
| BE |
| BD |
3
| ||
| 10 |
解答:证明:(Ⅰ)方法1(几何法):
连接BD、AC,交点为O.
∵ABCD是正方形
∴BD⊥AC …(2分)
∵AF⊥平面ABCD
∴AF⊥BD …(4分)
又∵AC∩AF=A,AC,AF?平面ACEF
∴BD⊥平面ACEF …(6分)
又∵EF?平面ACEF
∴BD⊥EF …(7分)
方法2:如图建立空间直角坐标系A-xyz,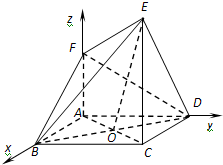
∵B(1,0,0),D(0,1,0)
∴
=(-1,1,0)…(2分)
设F(0,0,h),那么E(1,1,λh),…(4分)
则
=(-1,-1,(1-λ)h) …(5分)
∴
•
=0
∴BD⊥EF …(7分)
(Ⅱ)方法1:连接OE,由(Ⅰ)方法1知,BD⊥平面ACEF,
所以∠BEO即为直线BE与平面ACE所成的角. …(10分)
∵AF⊥平面ABCD,CE∥AF,
∴CE⊥平面ABCD,CE⊥BC,
∵BC=1,AF=1,则CE=λ,BE=
,BO=
,
∴Rt△BEO中,sin∠BEO=
=
=
,…(13分)
因为λ>1,解得λ=
. …(15分)
方法2:∵
=(0,1,λ),由(Ⅰ)法1知,BD⊥平面ACEF,
故
=(-1,1,0)是平面ACE的法向量. …(10分)
记直线BE与面ACE所成角为θ,
则sinθ=
=
=
…(13分);
因为λ>1,解得λ=
…(15分)
连接BD、AC,交点为O.
∵ABCD是正方形
∴BD⊥AC …(2分)
∵AF⊥平面ABCD
∴AF⊥BD …(4分)
又∵AC∩AF=A,AC,AF?平面ACEF
∴BD⊥平面ACEF …(6分)
又∵EF?平面ACEF
∴BD⊥EF …(7分)
方法2:如图建立空间直角坐标系A-xyz,

∵B(1,0,0),D(0,1,0)
∴
| BD |
设F(0,0,h),那么E(1,1,λh),…(4分)
则
| EF |
∴
| BD |
| EF |
∴BD⊥EF …(7分)
(Ⅱ)方法1:连接OE,由(Ⅰ)方法1知,BD⊥平面ACEF,
所以∠BEO即为直线BE与平面ACE所成的角. …(10分)
∵AF⊥平面ABCD,CE∥AF,
∴CE⊥平面ABCD,CE⊥BC,
∵BC=1,AF=1,则CE=λ,BE=
| 1+λ2 |
| ||
| 2 |
∴Rt△BEO中,sin∠BEO=
| EO |
| BE |
| ||
2
|
3
| ||
| 10 |
因为λ>1,解得λ=
| 4 |
| 3 |
方法2:∵
| BE |
故
| BD |
记直线BE与面ACE所成角为θ,
则sinθ=
|
| ||||
|
|
| 1 | ||||
|
3
| ||
| 10 |
因为λ>1,解得λ=
| 4 |
| 3 |
点评:本题主要考查空间点、线、面位置关系,线面所成角等基础知识,同时考查空间想象能力和推理论证能力.建立空间坐标系,将空间直线与平面夹角问题转化为向量夹角问题,是解答的关键.

练习册系列答案
相关题目
 如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a.
如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a. 如图,已知ABCD是底角为30°的等腰梯形,AD=2
如图,已知ABCD是底角为30°的等腰梯形,AD=2 如图,已知ABCD是矩形,PD⊥平面ABCD,PB=2,PB与平面ABCD所成的角为30°,PB与平面PCD所成的角为45°,求:
如图,已知ABCD是矩形,PD⊥平面ABCD,PB=2,PB与平面ABCD所成的角为30°,PB与平面PCD所成的角为45°,求: 如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE.
如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE.