题目内容
 如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE.
如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE.(Ⅰ)求证:平面AEC⊥平面AFC;
(Ⅱ)求直线EC与平面BCF所成的角;
(Ⅲ)问在EF上是否存在一点M,使三棱锥M-ACF是正三棱锥?若存在,试确定M点的位置;若不存在,说明理由.
分析:(I)以D为坐标原点,DA,DC,DE分别为X,Y,Z轴正言论自由建立空间直角坐标系,分别求出各点坐标,进而求出平面AEC和平面AFC的法向量的坐标,代入向量夹角公式,根据两个法向量的数量积为0,即可得到平面AEC⊥平面AFC;
(II)求出直线EC的方向向量及平面BCF的法向量,代入向量夹角公式,即可得到直线EC与平面BCF所成的角;
(Ⅲ)在EF上存在满足FM=2ME一点M,使M-ACF是正三棱锥,由已知可得ACF是一个正三角形,只须M在平面ACF上的投影,为三角形ACF的中心即可.
(II)求出直线EC的方向向量及平面BCF的法向量,代入向量夹角公式,即可得到直线EC与平面BCF所成的角;
(Ⅲ)在EF上存在满足FM=2ME一点M,使M-ACF是正三棱锥,由已知可得ACF是一个正三角形,只须M在平面ACF上的投影,为三角形ACF的中心即可.
解答: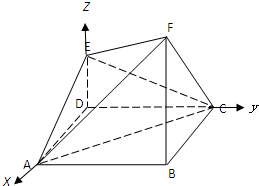 证明:(I)建立如图坐标系,令AB=FB=2DE=2
证明:(I)建立如图坐标系,令AB=FB=2DE=2
∴D(0,0,0),E(0,0,1),A(2,0,0),C(0,2,0),F(2,2,2)
∴
=(-2,0,1),
=(0,2,-1),
=(0,2,2),
=(-2,0,-2)
设
为面AEC法向量
=(x1,y1,z1)
则
⇒
=(1,1,2),
设
为面AFC法向量
=(x2,y2,z2)
则
⇒
=(1,1,-1)
∴cos<
•
>=
=0
∴
⊥
.
∴面AEC⊥面AFC.
(Ⅱ)∵
=(0,2,-1),
=(-2,0,-2),
=(0,0,-2)
设平面FBC的法向量为
=(a,b,c)
则
⊥
,且
⊥
,
即
,令b=1
则
=(0,1,0)
设直线EC与平面BCF所成的角为θ
则sinθ=
=
=
即直线EC与平面BCF所成的角为arcsin
(Ⅲ)在EF上存在满足FM=2ME一点M,使M-ACF是正三棱锥
作法:题意知△ACF是正三角形,
顶点M在ACF上的射影是△ACF的中心N
正方形的中心(即AC与BD的交点)为O,
则点N一定在OF上,且FN=2ON,
在平面EOF中过N作NM∥OE交EF于点M,
则该点为所求
 证明:(I)建立如图坐标系,令AB=FB=2DE=2
证明:(I)建立如图坐标系,令AB=FB=2DE=2∴D(0,0,0),E(0,0,1),A(2,0,0),C(0,2,0),F(2,2,2)
∴
| AE |
| EC |
| AF |
| FC |
设
| m |
| m |
则
|
| m |
设
| n |
| n |
则
|
| n |
∴cos<
| m |
| n |
| 1+1-2 | ||||
|
∴
| m |
| n |
∴面AEC⊥面AFC.
(Ⅱ)∵
| EC |
| FC |
| FB |
设平面FBC的法向量为
| v |
则
| v |
| FC |
| v |
| FB |
即
|
则
| v |
设直线EC与平面BCF所成的角为θ
则sinθ=
|
| ||||
|
|
| 2 | ||
|
2
| ||
| 5 |
即直线EC与平面BCF所成的角为arcsin
2
| ||
| 5 |
(Ⅲ)在EF上存在满足FM=2ME一点M,使M-ACF是正三棱锥
作法:题意知△ACF是正三角形,
顶点M在ACF上的射影是△ACF的中心N
正方形的中心(即AC与BD的交点)为O,
则点N一定在OF上,且FN=2ON,
在平面EOF中过N作NM∥OE交EF于点M,
则该点为所求
点评:本题考查的知识点是平面与平面垂直的判定,棱锥的结构特征,直线与平面所成的角,其中建立空间坐标系,将直线与平面的关系转化为向量的夹角问题,是解答本题的关键.

练习册系列答案
相关题目
 如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a.
如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a. 如图,已知ABCD是底角为30°的等腰梯形,AD=2
如图,已知ABCD是底角为30°的等腰梯形,AD=2 如图,已知ABCD是边长为1的正方形,AF⊥平面ABCD,CE∥AF,CE=λAF(λ>1).
如图,已知ABCD是边长为1的正方形,AF⊥平面ABCD,CE∥AF,CE=λAF(λ>1). 如图,已知ABCD是矩形,PD⊥平面ABCD,PB=2,PB与平面ABCD所成的角为30°,PB与平面PCD所成的角为45°,求:
如图,已知ABCD是矩形,PD⊥平面ABCD,PB=2,PB与平面ABCD所成的角为30°,PB与平面PCD所成的角为45°,求: