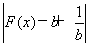题目内容
已知函数f(x)＝
.
(1)确定y＝f(x)在(0，＋∞)上的单调性；
(2)若a>0，函数h(x)＝xf(x)－x－ax2在(0,2)上有极值，求实数a的取值范围．
（1）在(0，e]上单调递增，在[e，＋∞)上单调递减．（2）a>－
（3）(0，＋∞)
【解析】(1)对已知函数f(x)求导得，f′(x)＝
.
由1－ln x＝0，得x＝e.
∴当x∈(0，e)时，f′(x)>0；当x∈(e，＋∞)时，f′(x)<0，
∴函数f(x)在(0，e]上单调递增，在[e，＋∞)上单调递减．
(2)由h(x)＝xf(x)－x－ax2，
可得h(x)＝ln x－x－ax2，
则h′(x)＝
－1－2ax＝
.
h(x)＝xf(x)－x－ax2在(0,2)上有极值的充要条件是φ(x)＝－2ax2－x＋1在(0,2)上有零点，
∴φ(0)·φ(2)<0，解得a>－.
综上所述，a的取值范围是(0，＋∞)．
练习册系列答案
相关题目
