题目内容
【题目】已知圆![]() ,过原点的直线
,过原点的直线![]() 与其交于不同的两点
与其交于不同的两点![]() .
.
(1)求直线![]() 斜率
斜率![]() 的取值范围;
的取值范围;
(2)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)若直线![]() 与曲线
与曲线![]() 只有一个公共点,求
只有一个公共点,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
试题分析:(1)直线![]() 与其交于不同的两点
与其交于不同的两点![]() ,
,![]() ,可得
,可得![]() ,即可求直线
,即可求直线![]() 斜率
斜率![]() 的取值范围;(2)利用
的取值范围;(2)利用![]() ,即可求线段
,即可求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;(3)利用直线
的方程;(3)利用直线![]() 与曲线
与曲线![]() 只有一个公共点,分类讨论,即可求
只有一个公共点,分类讨论,即可求![]() 的取值范围.
的取值范围.
试题解析:(1)由![]() 得
得![]()
直线![]() 过原点,可设其方程:
过原点,可设其方程:![]()
∵直线![]() 与其将于不同的两点
与其将于不同的两点![]() ∴
∴![]() ∴
∴![]()
(2)设点![]() ,∵点
,∵点![]() 为线段
为线段![]() 的中点,
的中点,
而曲线![]() 是圆心为
是圆心为![]() ,半径
,半径![]() 的圆,∴
的圆,∴![]()
∴![]() (
(![]() 且
且![]() )化简得
)化简得![]() ①
①
由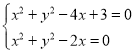 得
得![]()
![]() 是不同的两点,且点
是不同的两点,且点![]() 的坐标满足①
的坐标满足①
因此点![]() 满足
满足![]() ②
②
这是圆心为![]() ,半径为
,半径为![]() 的一段圆弧(不包括端点
的一段圆弧(不包括端点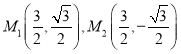 ),反之,可验证以方程②的解
),反之,可验证以方程②的解![]() 为坐标的点
为坐标的点![]() 是曲线
是曲线![]() 上的一个点,因此②是轨迹
上的一个点,因此②是轨迹![]() 的方程.
的方程.
(3)设直线![]() 过
过![]()
设直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ,则有
,则有![]() ,解得
,解得![]()
直线![]() 的斜率为
的斜率为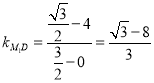
类似的可得![]()
综上,若直线![]() 与曲线
与曲线![]() 只有一个公共点,
只有一个公共点,
则![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.

练习册系列答案
相关题目


