题目内容
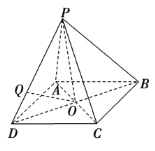
【题目】一个四棱锥的三视图如图所示.

(1)求证:PA⊥BD;
(2)在线段PD上是否存在一点Q,使二面角Q-AC-D的平面角为30°?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)详见解析(2)![]() =
=![]() .
.
【解析】
试题分析:(1)由三视图,可知四棱锥的底面是正方形,侧面是全等的等腰三角形,所以该四棱锥是一个正四棱锥.作出它的直观图,根据线面垂直的判定与性质,可证出PA⊥BD;(2)假设存在点Q,使二面角Q-AC-D的平面角为30°,由AC⊥平面PBD可得∠DOQ为二面角Q-AC-D的平面角,可证出在Rt△PDO中,OQ⊥PD,且∠PDO=60°,结合三角函数的计算可得![]() =
=![]() .
.
试题解析:(1)由三视图可知P-ABCD为四棱锥,底面ABCD为正方形,且PA=PB=PC=PD,连接AC、BD交于点O,连接PO.
因为BD⊥AC,BD⊥PO,所以BD⊥平面PAC,
即BD⊥PA.
(2)由三视图可知,BC=2,PA=2![]() ,假设存在这样的点Q,因为AC⊥OQ,AC⊥OD,
,假设存在这样的点Q,因为AC⊥OQ,AC⊥OD,
所以∠DOQ为二面角Q-AC-D的平面角,
在△POD中,PD=2![]() , OD=
, OD=![]() ,则∠PDO=60°,
,则∠PDO=60°,
在△DQO中,∠PDO=60°,且∠QOD=30°.
所以DP⊥OQ.所以OD=![]() ,QD=
,QD=![]() .
.
所以![]() =
=![]() .
.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目


