题目内容
已知数列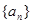 的前
的前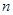 项和
项和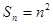 ,数列
,数列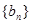 满足
满足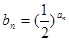
(1)求数列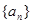 的通项公式
的通项公式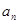 ;(2)求数列
;(2)求数列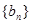 的前
的前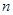 项和
项和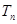 ;
;
(3)求证:不论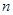 取何正整数,不等式
取何正整数,不等式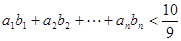 恒成立
恒成立
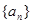 的前
的前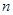 项和
项和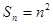 ,数列
,数列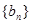 满足
满足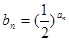
(1)求数列
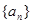 的通项公式
的通项公式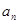 ;(2)求数列
;(2)求数列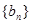 的前
的前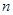 项和
项和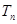 ;
;(3)求证:不论
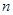 取何正整数,不等式
取何正整数,不等式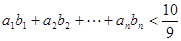 恒成立
恒成立(1)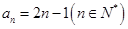
(2)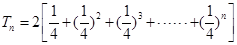
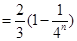 ;
;
(3)错位相减得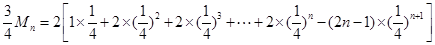
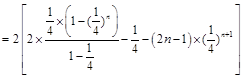
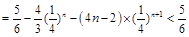 得到
得到 .
.
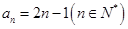
(2)
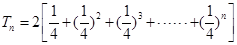
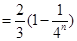 ;
;(3)错位相减得
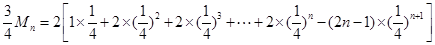
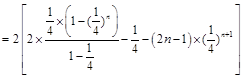
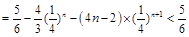 得到
得到 .
. 试题分析:(1)
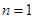 时,
时,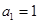
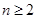 时,
时,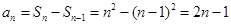 ,
, 故
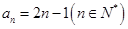
(2)∵
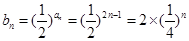 ,∴数列{
,∴数列{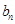 }是以
}是以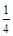 为公比的等比数列. 8分
为公比的等比数列. 8分∴
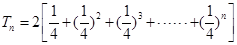
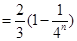 10分
10分(3)记
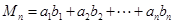
即
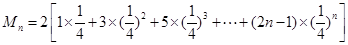
则
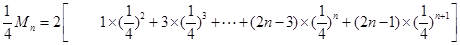
作差得
 12分
12分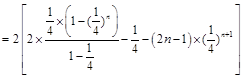
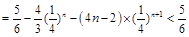 14分
14分故
 . 16分
. 16分点评:中档题,本题具有较强的综合性,本解答从确定通项公式入手,认识到数列的特征,利用“错位相消法”先求和,再“放缩”,达到证明目的。“分组求和法”“裂项相消法”“错位相减法”是高考常常考到数列求和方法。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
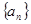 中,
中,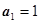 ,前
,前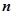 项的和为
项的和为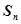 ,对任意的
,对任意的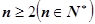 ,
,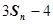 ,
,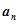 ,
,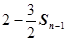 总成等差数列.
总成等差数列.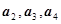 的值并猜想数列
的值并猜想数列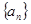 的通项公式
的通项公式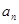
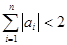 .
.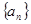 为等差数列,
为等差数列,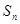 是其前n项的和,且
是其前n项的和,且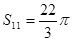 ,则
,则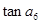 =( )
=( )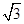

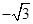

 中,若
中,若 ,则
,则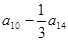 =( )
=( )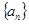 前
前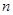 项和为
项和为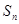 ,且
,且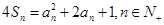 .
.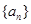 的通项公式;
的通项公式;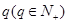 的等比数列
的等比数列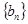 满足
满足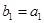 ,且存在
,且存在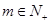 满足
满足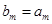 ,
,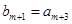 ,求数列
,求数列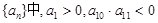 ,若此数列的前10项和
,若此数列的前10项和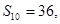 前18项和
前18项和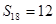 ,则数列
,则数列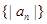 的前18项和
的前18项和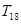 的值是
的值是  满足
满足 ,且
,且 ,则
,则
 ( ).
( ).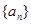 中,
中,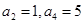 ,则
,则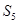 =( )
=( )