题目内容
【题目】已知平面五边形
是轴对称图形(如图1)，BC为对称轴，AD⊥CD，AD=AB=1，
，将此五边形沿BC折叠，使平面ABCD⊥平面BCEF，得到如图2所示的空间图形，对此空间图形解答下列问题.
（1）证明：AF∥平面DEC；
（2）求二面角
的余弦值.
【答案】见解析
【解析】（1）如图，过D作DG⊥BC于点G，连接GE，
因为BC为对称轴，所以AB⊥BC，则有AB∥DG，又AB平面ABF，
所以DG∥平面ABF，同理EG∥平面ABF.又DG∩EG=G，所以平面DGE∥平面ABF.
又平面AFED∩平面ABF=AF，平面AFED∩平面DGE=DE，所以AF∥DE，
又DE平面DEC，所以AF∥平面DEC.
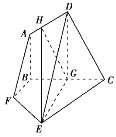
（2）如图，过G作GH⊥AD于点H，连接HE.由（1）知EG⊥BC，又平面ABCD⊥平面BCEF，平面ABCD∩平面BCEF=BC，所以EG⊥平面ABCD，所以EG⊥AD.
又EG∩HG=G，所以AD⊥平面EHG，则AD⊥HE，
则∠EHG即为二面角
的平面角.
由AD⊥CD，AD=AB=1，
，得G为BC的中点，
，
，
.
因为
为直角三角形，所以
，
则二面角的余弦值为
.
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
【题目】某单位共有10名员工，他们某年的收入如下表：
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪（万元） | 3 | 3.5 | 4 | 5 | 5.5 | 6.5 | 7 | 7.5 | 8 | 50 |
（1）从该单位中任取2人，此2人中年薪收入高于5万的人数记为
，求
的分布列和期望；
（2）已知员工年薪收入
与工作所限
成正相关关系，某员工工作第一年至第四年的年薪如下表：
工作年限 | 1 | 2 | 3 | 4 |
年薪（万元） | 3.0 | 4.2 | 5.6 | 7.2 |
预测该员工第五年的年薪为多少？
附：线性回归方程
中系数计算公式和参考数据分别为：
，
，其中
为样本均值，
，
，（
）
