题目内容
13. 已知四棱锥P-ABCD底面是平行四边形,E,F分别为AD,PC的中点,
已知四棱锥P-ABCD底面是平行四边形,E,F分别为AD,PC的中点,EF⊥BD,2AP=2AB=AD,以AD为直径的圆经过点B.
(Ⅰ)求证:平面PAB⊥平面ABCD;
(Ⅱ)若AB=PB=2.求三棱锥C-BEF的体积.
分析 (I)如图所示,取PB的中点G,连接AG,FG,利用三角形中位线定理可得:四边形AEFG是平行四边形,可得EF∥AC,可得AG⊥BD.由以AD为直径的圆经过点B,
可得BD⊥AB.可得DB⊥平面PAB,即可平面PAB⊥平面ABCD;
(II)取AB的中点H,连接PH,利用正三角形可得:PH⊥AB.PH=$\sqrt{3}$.又F是PC的中点,可得点F到平面ABCD的距离d=$\frac{1}{2}$PH,由BD⊥AB,可得BD=$\sqrt{A{D}^{2}-A{B}^{2}}$,可得点B到AD的距离h=$\frac{AB•BD}{AD}$,S△BCE=$\frac{1}{2}BC•h$.利用VC-BEF=VF-BCE=$\frac{1}{3}d•{S}_{△BCE}$即可得出.
解答 (I)证明:如图所示,取PB的中点G,连接AG,FG,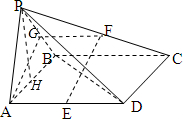
由已知可得FG$\underset{∥}{=}\frac{1}{2}BC$,
∵AE$\underset{∥}{=}\frac{1}{2}BC$,∴FG$\underset{∥}{=}$AE.
∴四边形AEFG是平行四边形,
∴EF∥AC,
∵EF⊥BD,∴AG⊥BD.
∵以AD为直径的圆经过点B,
∴BD⊥AB.
又AG∩AB=A,∴DB⊥平面PAB,
又DB?平面ABCD,∴平面PAB⊥平面ABCD;
(II)解:取AB的中点H,连接PH,
∵AP=AB=BP=2,
∴PH⊥AB.PH=$\sqrt{3}$.
又F是PC的中点,
∴点F到平面ABCD的距离d=$\frac{\sqrt{3}}{2}$,
∵BD⊥AB,∴BD=$\sqrt{A{D}^{2}-A{B}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴点B到AD的距离h=$\frac{AB•BD}{AD}$=$\frac{2×2\sqrt{3}}{4}$=$\sqrt{3}$,
∴S△BCE=$\frac{1}{2}BC•h$=$\frac{1}{2}×4×\sqrt{3}$=2$\sqrt{3}$.
∴VC-BEF=VF-BCE=$\frac{1}{3}d•{S}_{△BCE}$=$\frac{1}{3}×\frac{\sqrt{3}}{2}×2\sqrt{3}$=1.
点评 本题考查了线面平行垂直的判定与性质定理、平行四边形的性质、正三角形的性质、“等积变形”、三棱锥的体积计算公式,考查了推理能力与体积计算公式,属于中档题.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| A. | 3 | B. | 4 | C. | 7 | D. | 8 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条既 |
| A. | $\frac{4\sqrt{2}π}{3}$ | B. | $\frac{16\sqrt{2}π}{3}$ | C. | $\frac{32\sqrt{2}π}{3}$ | D. | $\frac{64\sqrt{2}π}{3}$ |
 若某市8所中学参加中学生合唱比赛的得分用茎叶图表示如图,其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
若某市8所中学参加中学生合唱比赛的得分用茎叶图表示如图,其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )| A. | 91 5.5 | B. | 91 5 | C. | 92 5.5 | D. | 92 5 |