题目内容
8.已知四棱锥S-ABCD的所有顶点在同一球面上,底面ABCD是正方形且球心O在此平面内,当四棱锥体积取得最大值时,其面积等于16+16$\sqrt{3}$,则球O的体积等于( )| A. | $\frac{4\sqrt{2}π}{3}$ | B. | $\frac{16\sqrt{2}π}{3}$ | C. | $\frac{32\sqrt{2}π}{3}$ | D. | $\frac{64\sqrt{2}π}{3}$ |
分析 当此四棱锥体积取得最大值时,四棱锥为正四棱锥,根据该四棱锥的表面积等于16+16$\sqrt{3}$,确定该四棱锥的底面边长和高,进而可求球的半径为R,从而可求球的体积.
解答 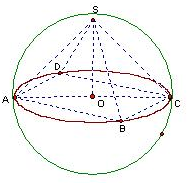 解:由题意,当此四棱锥体积取得最大值时,四棱锥为正四棱锥,
解:由题意,当此四棱锥体积取得最大值时,四棱锥为正四棱锥,
∵该四棱锥的表面积等于16+16$\sqrt{3}$,
设球O的半径为R,则AC=2R,SO=R,如图,
∴该四棱锥的底面边长为AB=$\sqrt{2}$R,
则有($\sqrt{2}$R)2+4×$\frac{1}{2}$×$\sqrt{2}$R×$\sqrt{(\frac{\sqrt{2}}{2}R)^{2}+{R}^{2}}$=16+16$\sqrt{3}$,
解得R=2$\sqrt{2}$
∴球O的体积是$\frac{4}{3}$πR3=$\frac{64\sqrt{2}}{3}$π.
故选:D.
点评 本题考查球内接多面体,球的体积,解题的关键是确定球的半径,再利用公式求解.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
16.已知函数f(x)=$\frac{lnx}{x}$-x2+2ex-k有且只有一个零点,则k的值为( )
| A. | e+$\frac{1}{{e}^{2}}$ | B. | e+$\frac{1}{e}$ | C. | e2+$\frac{1}{e}$ | D. | e2+$\frac{1}{{e}^{2}}$ |
20.执行如图所示的程序框图,则输出的z的值是( )


| A. | 21 | B. | 32 | C. | 34 | D. | 64 |
 如图是绵阳市某小区100户居民2014年月平均用水量(单位:t)的频率分布直方图的一部分,则该小区2014年的月平均用水量的中位数的估计值为2.02.
如图是绵阳市某小区100户居民2014年月平均用水量(单位:t)的频率分布直方图的一部分,则该小区2014年的月平均用水量的中位数的估计值为2.02. 已知四棱锥P-ABCD底面是平行四边形,E,F分别为AD,PC的中点,
已知四棱锥P-ABCD底面是平行四边形,E,F分别为AD,PC的中点, 如图,已知圆O半径是3,PAB和PCD是圆O的两条割线,且PAB过O点,若PB=10,PD=8,给出下列四个结论:
如图,已知圆O半径是3,PAB和PCD是圆O的两条割线,且PAB过O点,若PB=10,PD=8,给出下列四个结论: