题目内容
11．如图是某几何体的三视图，则该几何体的表面积是（ ）
| A． | 2$\sqrt{3}$+$\frac{3\sqrt{7}}{2}$ | B． | 2$\sqrt{3}$+$\sqrt{15}$ | C． | 2$\sqrt{3}$+2$\sqrt{15}$ | D． | 2$\sqrt{3}$+3$\sqrt{7}$ |
分析 由已知中的三视图，可知该几何体是以俯视图为底面的三棱锥，求出棱锥各个面的面积，相加可得答案．
解答 解：由已知中的三视图，可知该几何体是以俯视图为底面的三棱锥，
其直观图如下图所示：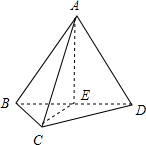
面ABD和面BCD都是边长为2的等边三角形，故面积为：$\sqrt{3}$，
AE=CE=$\sqrt{3}$，AC=$\sqrt{6}$，
故面ABC和面ACD均是腰长为2，底为$\sqrt{6}$的等腰三角形，
故底上的高为：$\sqrt{{2}^{2}-（\frac{\sqrt{6}}{2}）^{2}}$=$\frac{\sqrt{10}}{2}$，
故面ABC和面ACD的面积均为：$\frac{\sqrt{15}}{2}$，
故该几何体的表面积S=2$\sqrt{3}$+$\sqrt{15}$，
故选：B
点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
相关题目
1．已知抛物线y2=2px（p＞0），直线AB经过抛物线的焦点为F，则∠AOB的可能值为（ ）
| A． | $\frac{π}{2}$ | B． | $\frac{2π}{3}$ | C． | $\frac{3π}{4}$ | D． | $\frac{5π}{6}$ |
在三棱锥A-BCD中，底面BCD是正三角形，AC=BD=2，AB=AD=$\sqrt{2}$，O为BC的中点．
16．某几何体的正视图，侧视图及俯视图均如图所示，则该几何体的体积为（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{8}{3}$ | C． | $\sqrt{6}$ | D． | 2$\sqrt{6}$ |
3．“m=1”是“?x∈（0，+∞），m≤x+$\frac{1}{x}$-1”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |