题目内容
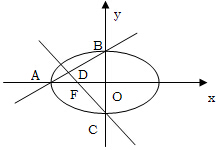 如图所示,椭圆
如图所示,椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据椭圆的离心率得到a,b,c之间的关系,利用这些关系表示出∠BAO、∠CFO的正切值,根据图得角之间的关系:∠BDC=∠BAO+∠CFO,利用正切公式求出tan∠BDC的值.
解答:
解:由题意得离心率e=
=
,则设c=k,a=2k(k>0),
由a2=b2+c2得,b2=a2-c2=3k2,解得b=
k,
由图可知,∠ DFA=∠CFO,且∠BDC=∠BAO+∠DFA,
DFA=∠CFO,且∠BDC=∠BAO+∠DFA,
所以∠BDC=∠BAO+∠CFO,
又tan∠BAO=
=
=
,tan∠CFO=
=
=
,
则tan∠BDC=tan(∠BAO+∠OFC)=
=
=-3
,
所以tan∠BDC的值是-3
.
| c |
| a |
| 1 |
| 2 |
由a2=b2+c2得,b2=a2-c2=3k2,解得b=
| 3 |
由图可知,∠
 DFA=∠CFO,且∠BDC=∠BAO+∠DFA,
DFA=∠CFO,且∠BDC=∠BAO+∠DFA,所以∠BDC=∠BAO+∠CFO,
又tan∠BAO=
| OB |
| OA |
| b |
| a |
| ||
| 2 |
| OC |
| OF |
| b |
| c |
| 3 |
则tan∠BDC=tan(∠BAO+∠OFC)=
| tan∠BAO+tan∠CFO |
| 1-tan∠BAOtan∠CFO |
=
| ||||||
1-
|
| 3 |
所以tan∠BDC的值是-3
| 3 |
点评:本题考查椭圆的简单性质的应用,两角和差的正切函数,由图得到tan∠BDC=tan(∠BAO+∠OFC)是解题的难点和关键.

练习册系列答案
相关题目
点A(1,-2)在直线xcosθ-
y-4=0的( )
| 2 |
| A、上方 | B、下方 |
| C、线上 | D、位置视θ而定 |
在等差数列{an}中,a10<0,a11>0,且a11>|a10|,则{an}的前n项和Sn中最大的负数为( )
| A、S17 |
| B、S18 |
| C、S19 |
| D、S20 |
已知平面向量
=(2m+1,3)
=(2,m),且
∥
,则实数m的值等于( )
| a |
| b, |
| a |
| b |
A、2或-
| ||
B、
| ||
C、-2或
| ||
D、-
|