Question

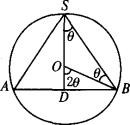
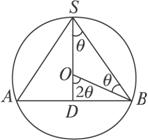
已知球的体积为V，在它里面有一个轴截面顶角为2q的内接圆锥(如图)，求圆锥的体积．

 

Answer 1

答案：
解析：

解：设圆锥的底面半径为r，球心O到圆锥底面距离为x， 则有r=Rsin2q，x=Rcos2q． ∴V圆锥=πr2·(R＋x)=R2sin2q(R＋Rcos2q) =πR3(sin22q·cos2q)=Vsin22qcos2q．